 Leetcode (13) - Hot 100 热门 100 题
Leetcode (13) - Hot 100 热门 100 题
重新开刷 leetcode。这次按照 Hot 100 的专题来,之前已经做过的就再重复啦。 Hot 100 大概还剩余 50 多题没有做。
# 4 - 寻找两个有序数组的中位数
# 问题
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
2
3
4
# 思路
看到这个复杂度,想必是要用二分之类的递归来做了,直接合并两个有序数组的话,复杂度就是 m+n 级别的了。
详细说明可以参考下 这个leetcode题解 (opens new window).
这里结合下面代码记录下思路。首先调整两个数组,让A是较短的那个,B是较长的那个。A长度为m,B长度为n。
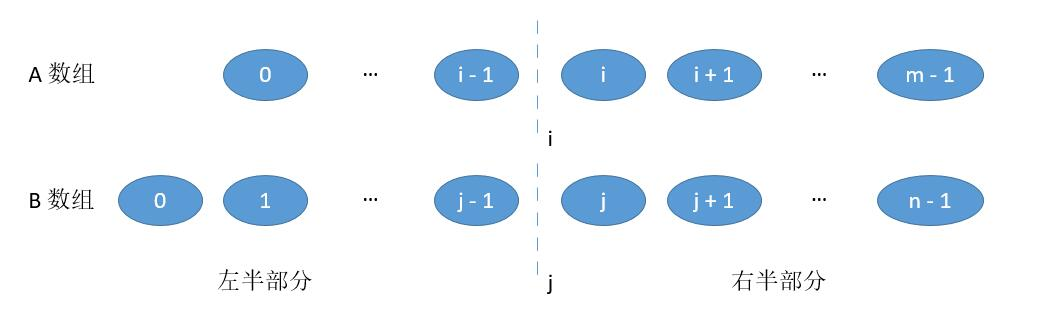
我们要找到两个切分点i和j,分别把AB切成两块,同时两个左边部分汇总成左半部分,两个右边汇总成右半部分。
理想的切分后,如果m+n总长度为偶数,则希望两边元素个数相等,中位数就是左边的最大值和右边的最小值的平均。如果m+n总长度为奇数,希望左边元素比右边元素多1个,那么中位数就是左边的最大值。
那么现在问题在于,如何找到正确的i和j,使之能满足上面的条件(左右两边元素个数相等,且左边均小于右边)。
为了保证左右两边个数相等,i和j要满足这个关系: j = (m+n+1)//2 - i,也就是 i+j应该等于 m+n的一半。
为了保证左边均小于右边,就需要按情况来处理。首先肯定有A[i-1] < A[i],也肯定有 B[j-1] < B[j]。但是可能出现 A[i-1] > B[j]的情况,此时i应当往左移动,相应地 j也就会往右移动。同理,出现B[j-1] > A[i]的情况,此时i应该往右移动,相应的j也就会往左移动。
i左右移动的时候,就可以通过二分的方式,比如说i需要往左移动,那么我们取 i = (0 + i-1) // 2。通过这种二分的方式,实现了log级别的复杂度。
此外也要考虑一种边界的情况,一个是 i=0或者j=0,此时说明有某一个数组完全被划分到了一边,i=0时,左半边的最大值就是B[j-1],j=0时,左半边的最大值就是A[i-1]。同样,当 i=m或者j=n时,也是有某一个数组被完全划分到了一边,当i=m时,右半边的最小值就是B[j], 当j=n时,右半边的最小值就是A[i]。
下面来对照代码理解下:
# 代码
# 注意,下面是python2的代码,注意和3在 / 和 // 上的不同
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
A, B = nums1, nums2
m, n = len(A), len(B)
if m > n:
A, B, m, n = B, A, n ,m
if n == 0:
return None
# 初始,i的范围是 0 到 m
imin, imax, half_len = 0, m , (m + n + 1) / 2
while imin <= imax:
i = (imin + imax) / 2 # i 取当前可取区间的中间点
j = half_len - i # 根据 ij 之间的关系,根据i来计算出j
if i < m and j > 0 and B[j-1] > A[i]: # i需要增大 【1】
imin = i + 1
elif i > 0 and j < n and A[i-1] > B[j]: # i需要减小 【2】
imax = i - 1
else: # 达到左边均小于右边的要求 【3】
# 先求左边的最大值
if i == 0:
max_of_left = B[j-1]
elif j == 0:
max_of_left = A[i-1]
else:
max_of_left = max(A[i-1], B[j-1])
# 如果m+n是奇数的话,直接返回左边的最大值就是中位数了
if (m + n) % 2 == 1:
return max_of_left
# 否则还需要求右边的最小值,两者取平均作为中位数
if i == m:
min_of_right = B[j]
elif j == n:
min_of_right = A[i]
else:
min_of_right = min(A[i], B[j])
return (max_of_left + min_of_right) / 2.0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
说一下上面的【3】,为什么到【3】的情况下,就表明达到要求了呢,如果i或者j到达边缘的话( i,j=0或者i=m或者j=n)也会触发else。
个人想法:那以i=0举例吧,i=0肯定是说明i是不断减小不断减小,比如说
0 1 2 3 4 (m=4) m=3 m奇数偶数都一样
i=2
i=1 此时说明A[0] > B[j],i才会继续减小
i=0 此时j变大了,新j=旧j+1,A[0]不能保证仍然大于B[新j],但上面说过了 A[0]肯定大于B[旧j],而B[旧j]此时是左边最大的,所以A[0]大于左边最大的,的确是满足了右边的最小大于左边的最大。
2
3
4
再说下【1】和【2】,有下面的说明,所以可以简化if判断条件,只判断i是否越界就行,不用判断j
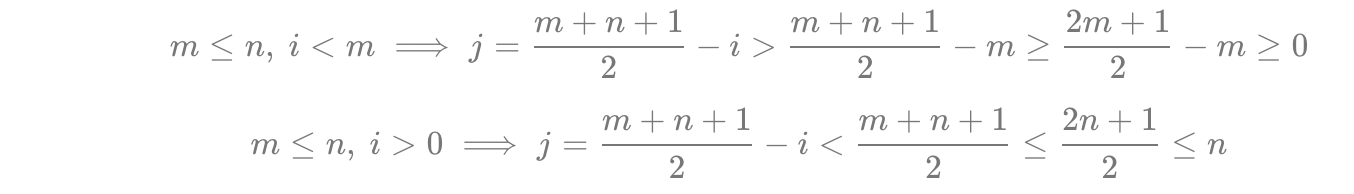
# 5 最长回文子串
# 问题
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
2
3
4
# 思路
详细可以参考Leetcode中的网友题解 (opens new window)
比较暴力的中心扩展法,对于 b|a|b|a|d ,最长回文子串可能是偶数长度(对称轴是某个|),也可能是奇数长度(对称轴是某个字母),所以可以从头到位依次考察每个可能是对称轴的位置,得到最长。那一共需要考察 2n-1 个位置,每个位置考察的长度为n,所以复杂度是 n^2 级别的。
Manacher算法,专门解决这个最长回文子串的问题,本质还是中心扩展法 ,类似于KMP字符串匹配,有类似剪枝的方法避免重复计算。不详细看这种方法了……
最长公共子串法。将原串倒置,然后求原串和倒置的最长公共子串。例如 babad,倒置 dabab,最长公共子串是 aba或者bab。注意这种方法有个问题,例如 abacdfgdcaba 倒置 abacdgfdcaba 最长公共子串是 abacd,但其实这个子串并不是回文。所以还需要判断找到的最长公共子串,在原串和倒置串中的下标是否满足对应关系。不满足,就得继续考察其他的公共子串。
详细说下 动态规划法。
使用 s[l, r]来表示以lr为边界的子串,dp[l][r]取值True False表示这一段是否是回文。
有状态转移方程:
dp[l, r] = ( s[l]==s[r] and (r-l<=2 or dp[l+1][r-1]) )
解释一下,就是如果短的串dp[l+1][r-1]是回文,例如 bcb,而两端同时往外扩展一个字符,这两个字符也相等,例如 abcba 的话,扩展出来的串也是回文。
另外,当 r-1和l+1相等时,说明短串只有一个字母,肯定是回文,例如长串 bcb 的情况,短串是c;而当 r-1还比l+1要小1的时候,说明短串是空的,也肯定是回文,例如长串是bb,短串是空的了。所以当r-1-(l+1) <=0也即 r-l <= 2时,说明短串也一定是回文,这时直接可以判定为True,这就是上面方程中 or 前面的部分的由来。
# 代码
class Solution:
def longestPalindrome(self, s: str) -> str:
size = len(s)
if size <= 1:
return s
dp = [[False] * size] * size
longest = 1
res = s[0]
for r in range(1, size):
for l in range(r):
if s[l] == s[r] and (r-l <= 2 or dp[l+1][r-1]):
dp[l][r] = True
cur_len = r - l + 1
if cur_len > longest:
longest = cur_len
res = s[l:r+1]
return res
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
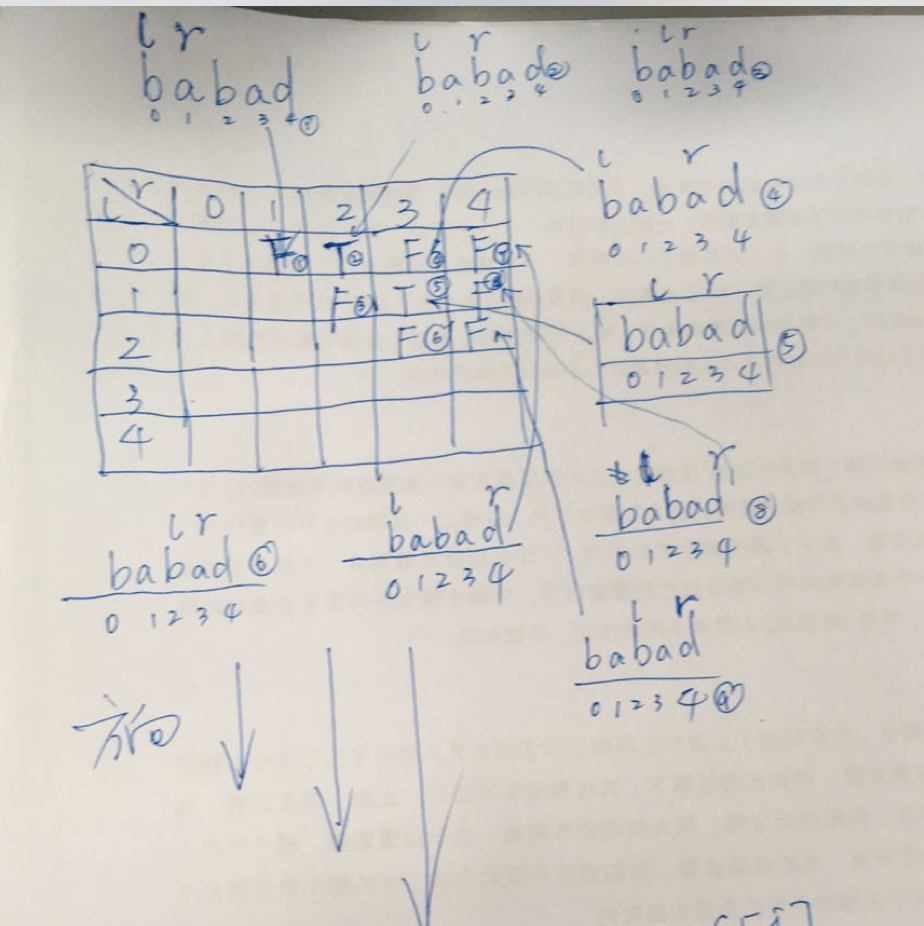
直接搬运题解中的一张图,上面代码执行时,类似于下图的效果;填充顺序是一列一列,从左到右每一列依次填写,每一列里面又是从上到下填写。
# 10 正则表达式匹配
# 问题
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 . 和 * 的正则表达式匹配。
. 匹配任意单个字符
* 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
说明: s 可能为空,且只包含从 a-z 的小写字母。 p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
示例 4:
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false
2
3
4
5
6
7
8
9
10
11
12
# 思路
一种是回溯法,思路比较简单,类似于穷举。如果没有遇到星号,则一个一个匹配,遇到带有星号的字符时,可以让带星号字符匹配当前字符,或者跳过星号,这两种情况,依次递归下去。找到任何一种匹配,则说明可以匹配。
回溯几乎穷举了各种情况,其复杂度会比较高。联想到回溯当中,有一些子串可能会被重复判断,可以加一个备忘录,使用 dp[i,j] 来表示 text[i:] 和 pattern[j:] 能否匹配,当遇到重复判断的情况时,直接从dp中取值即可。
# 代码
自顶向下递归版,带备忘录的回溯法:
class Solution:
def isMatch(self, text: str, pattern: str) -> bool:
memo = {}
def dp(i, j):
if (i, j) not in memo: # 如果memo中有,则直接用,memo没有,则递归计算
if j == len(pattern): # 如果同时到达末尾,匹配成功
ans = i == len(text)
else:
first_match = i < len(text) and pattern[j] in {text[i], '.'} # 判断首个字符是否匹配
if j + 1 < len(pattern) and pattern[j+1] == '*': # 如果pattern当前字符后面是星号
# 要么忽略星号,匹配0个字符;要么星号先匹配了当前字符,并保留星号继续匹配后面
ans = dp(i, j+2) or (first_match and dp(i+1, j))
else:
# 不是星号,则要求首个字符匹配,且继续匹配后面的字符
ans = first_match and dp(i+1, j+1)
memo[i, j] = ans # 存入memo
return memo[i, j]
return dp(0, 0)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
还有一个自底向上的版本,从后往前:
class Solution(object):
def isMatch(self, text, pattern):
dp = [[False] * (len(pattern) + 1) for _ in range(len(text) + 1)]
dp[-1][-1] = True
for i in range(len(text), -1, -1):
for j in range(len(pattern) - 1, -1, -1):
first_match = i < len(text) and pattern[j] in {text[i], '.'}
if j+1 < len(pattern) and pattern[j+1] == '*':
dp[i][j] = dp[i][j+2] or first_match and dp[i+1][j]
else:
dp[i][j] = first_match and dp[i+1][j+1]
return dp[0][0]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 11 盛最多水的容器
# 问题
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。每条线相当于一块木板,找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
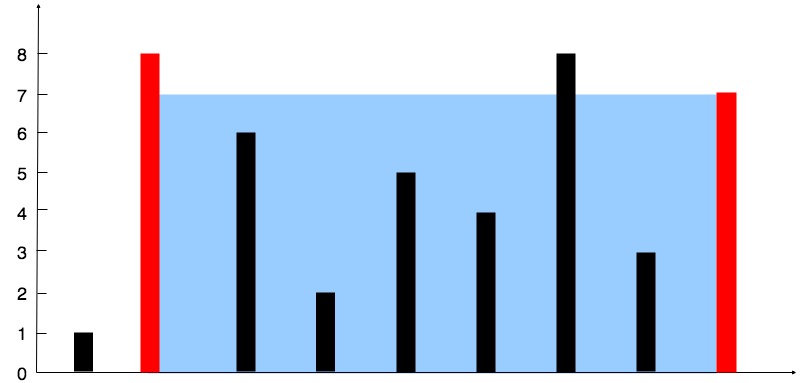
例如,图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
# 思路
既要让木板尽可能高,也得让它俩尽可能远离。暴力的方法容易想到,两两组合起来,计算容量,然后选最大即可,复杂度是n^2。
双指针法。两个指针分别指向两端,并算出此时容量,更新最大容量。然后,比较矮的指针向中间移动,继续计算容量并更新max,直到相遇。
为什么这种方法能够work呢?上面说过,容量取决于木板的高度,也取决于两块木板之间的距离。最开始的时候,两块木板之间的距离最大。总的容量,受限于矮的那一块,假如我们让高的一侧往里移动的话,距离缩小了,矮的那块仍然矮,总的容量肯定只会变小不会变大,但移动矮的话有可能会遇到更高的木板,使得总容量变大。
一点扩展:如果要找容量最小的呢?其实更简单,只需要找到最矮的那块板,然后任选它左右的1块就可以,此时距离最短,且高度最矮。
# 代码
class Solution:
def maxArea(self, height: List[int]) -> int:
if len(height) <= 1:
return 0
ret = -1
i, j = 0, len(height) - 1
while i < j:
ret = max(ret, (j - i) * min(height[i], height[j]))
if height[i] <= height[j]:
i += 1
else:
j -= 1
return ret
2
3
4
5
6
7
8
9
10
11
12
13
# 15 三数之和
# 问题
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
# 思路
联想到之前的 leetcode 第一题 —— 两数之和。最暴力的是三层循环去做,类似 two sum里 用一个hashmap来记录。
另外的方法是排序+双指针法。先将nums排序,从小到大,最外层循环固定指针k,然后在k右侧也是一个有序的,来找到i j 下标能够满足和为0。这当中又有一些技巧:
nums[k] 大于0时,直接结束外层循环,因为数组已有序,k右侧都是正数,不会满足和为0的条件了;
当 k 的前一个 k-1 和 k 位置的数相等时,跳过此k,因为再去搜的话,只会搜到和 k-1 处相同的重复结果;
i j分别指向k右侧部分的两端,根据 sum 和 0 的大小关系分别让i j往中间靠拢,当 sum > 0 时需要让 j向左,当小于0时需要让i向右。注意,移动ij时需要跳过重复值,避免得到重复结果。
整个的复杂度在 n^2 级别。
# 代码
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort() # 先排序
length = len(nums)
ans = []
if not nums or length < 3:
return ans
for i in range(0, length): # 最外层循环
if nums[i] > 0:
break
if i > 0 and nums[i] == nums[i-1]:
continue
l, r = i+1, length-1
while l < r:
s = nums[i] + nums[l] + nums[r]
if s == 0:
ans.append([nums[i], nums[l], nums[r]])
# while的作用是跳过和当前l r位置重复的值,避免添加重复的结果到ans里
while l < r and nums[l] == nums[l+1]:
l += 1
while l < r and nums[r] == nums[r-1]:
r -= 1
# 上面while只针对重复情况移动了指针,所以这里记得还要继续移动lr指针一次!
l += 1
r -= 1
elif s < 0:
l += 1
else:
r -= 1
return ans
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 17 - 电话号码的字母组合
# 问题
九宫格键盘中,2-9数字分别代表了一些英文字母。给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
2代表abc,3代表def,4代表ghi, 5代表jkl,6代表mno,7代表pqrs,8代表tuv,9代表wxyz
# 思路
排列组合穷举,可以递归来做
# 代码
class Solution:
def __init__(self):
self.mp = {
'2': ['a', 'b', 'c'],
'3': ['d', 'e', 'f'],
'4': ['g', 'h', 'i'],
'5': ['j', 'k', 'l'],
'6': ['m', 'n', 'o'],
'7': ['p', 'q', 'r', 's'],
'8': ['t', 'u', 'v'],
'9': ['w', 'x', 'y', 'z']
}
self.result = []
self.mem = []
self.digits = ''
def trace(self, start):
if start == len(self.digits):
self.result.append(''.join(self.mem))
else:
for l in self.mp[self.digits[start]]:
self.mem.append(l)
self.trace(start + 1)
self.mem.pop(-1)
def letterCombinations(self, digits: str) -> List[str]:
if digits:
self.digits = digits
self.trace(0)
return self.result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
使用python还有一种非常巧妙的写法,执行效率也很高,可以看看:
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
dic = {'2': 'abc',
'3': 'def',
'4': 'ghi',
'5': 'jkl',
'6': 'mno',
'7': 'pqrs',
'8': 'tuv',
'9': 'wxyz'}
n = len(digits)
if n <= 1:
return [i for i in dic.get(digits, '')]
result = [i for i in dic[digits[0]]]
for i in range(1, n):
result = [x+y for x in result for y in dic[digits[i]]]
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 19 删除链表的倒数第n个节点
# 问题
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例: 给定一个链表: 1->2->3->4->5, 和 n = 2. 当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明: 给定的 n 保证是有效的。 你能尝试使用一趟扫描实现吗?
# 思路
经典题,先让一个指针走过n步,然后另起一个指针指向头,两个一起走,快指针走到结尾时,慢指针指向的就是倒数第n个节点的前一个结点,此时可操作删除倒数第n个节点。
eg. n=2
[nh] - [1] - [2] - [3] - [4]
f,s
先让f走过2步
[nh] - [1] - [2] - [3] - [4]
s f
然后一起走到f的next为空
[nh] - [1] - [2] - [3] - [4]
s f
此时s指向的就是倒数第n个节点的前一个节点
2
3
4
5
6
7
8
9
10
11
12
这里一定要注意数字对应关系,不要找错了,也要注意先添加一个空的头节点,来使得删除头节点和删除其他节点的情况可以统一处理。原理简单,但实际代码还是要细心。
当然啦,这个题由于题目明确指出,不用判断n是否合法。
# 代码
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
nh = ListNode(-1)
nh.next = head
f, s = nh, nh
for i in range(0, n):
f = f.next
while f.next:
f = f.next
s = s.next
s.next = s.next.next
return nh.next
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 22 括号生成
# 问题
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
2
3
4
5
6
7
# 思路
相当于现在有2n个位置,每个位置可以放置左右括号,可以暴力穷举然后判断是否有效,这样当然非常低效率,所以可以用回溯的方法,参见下面代码1.
也可以用动态规划的方式。我们可以认为i=n时的情况,是从i=n-1时的情况,在最外层添加了一对括号之后得来的。所以有这样的状态转移公式:
"(" + 【i=p时所有括号的排列组合】 + ")" + 【i=q时所有括号的排列组合】
其中 p+q = n-1, p可以从0取到n-1,相应地q取n-1到0
2
3
# 代码
先写一个回溯法:
class Solution:
def __init__(self):
self.ans = []
def generateParenthesis(self, n: int) -> List[str]:
self.backtrack(n, '', 0, 0)
return self.ans
def backtrack(self, n, s, left, right):
if len(s) == 2 * n: # 完成一次2n长度的有效生成
self.ans.append(s)
return
if left < n: # 左括号个数小于n,说明可以继续使用左括号
self.backtrack(n, s+'(', left+1, right)
if right < left: # 右括号个数小于左括号,说明可以继续使用右括号
self.backtrack(n, s+')', left, right+1)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
按第二种方法的解法
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
total = []
total.append([None]) # n为0的情况
total.append(['()']) # n为1的情况
for i in range(2, n+1): # 从2到n,依次计算,第i次依赖于前面i-1次的结果
l = []
for j in range(i): # 让left+right=i,穷举left和right每一种取值情况
p = total[j]
q = total[i-1-j]
for k1 in p:
for k2 in q:
if k1 is None:
k1 = ''
if k2 is None:
k2 = ''
tmp = '(' + k1 + ')' + k2
l.append(tmp)
total.append(l)
return total[n]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 23 合并k个排序链表
# 问题
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度
# 思路
按合并两个链表的思路,每次需要比较每个链表的首节点,找到最小的并入结果中,所以每合并一个节点需要比较k次,复杂度是 kn(k是链表个数,n是总的全部的节点数量)
可以进行的优化是用一个大小为k的小根堆,每次堆顶元素append,并从其所在的队列中出队头加入堆中。堆的维护复杂度是 logk,所以总复杂度是 nlogk。
还可以用分治思想,先两两合并,链表数缩减一半;继续两两合并,直到合并成1个链表。总的分治层数是logk,每一层时也是遍历了全部的n个节点,所以复杂度是 nlogk
# 代码
分治的代码主要是要实现不重不漏的两两归并,可以参考一些写法。下面的写法1类似归并排序,递归下去:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
if not lists:return
n = len(lists)
return self.merge(lists, 0, n-1)
def merge(self,lists, left, right): # 这种写法类似归并排序
if left == right:
return lists[left]
mid = left + (right - left) // 2
l1 = self.merge(lists, left, mid)
l2 = self.merge(lists, mid+1, right)
return self.mergeTwoLists(l1, l2)
...... 略
2
3
4
5
6
7
8
9
10
11
12
也可以写成下面这样,这种写法类似希尔排序的感觉,interval逐渐变大
while interval < amount:
for i in range(0, amount - interval, interval * 2):
lists[i] = self.merge2Lists(lists[i], lists[i + interval])
interval *= 2
return lists[0] if amount > 0 else lists
2
3
4
5
也可以用堆的方式,代码:
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
from Queue import PriorityQueue # python2中的包
class Solution:
def mergeKLists(self, lists):
head = point = ListNode(-1)
q = PriorityQueue()
for l in lists:
if l:
q.put((l.val, l))
while not q.empty():
val, node = q.get()
point.next = node
point = point.next
node = node.next
if node:
q.put((node.val, node))
return head.next
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
注意python3 的不同:
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
from queue import PriorityQueue # 这里
class Solution:
def mergeKLists(self, lists):
head = point = ListNode(-1)
q = PriorityQueue()
for l in lists:
if l:
q.put((l.val, id(l), l)) #这里
while not q.empty():
val, _, node = q.get() #这里
point.next = node
point = point.next
node = node.next
if node:
q.put((node.val, id(node), node)) # 这里
return head.next
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 31 下一个排列
# 问题
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须原地修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1
2
3
# 思路
需要先把问题分析清楚。首先,如果整个序列都是降序的话,此时是没有下一个更大的排列的,例如【9,8,7,6,5】。
如果不是全降序的话,我们从右边往左找,找到第一对连续的两个数字 a[i-1], a[i],满足a[i-1] 比 a[i] 小。此时 i 及其右侧的元素都是降序的,已经是这一部分所能构成的最大排列了,所以我们需要对 i-1 位置的进行一些操作,增大 i-1 位置。例如 328541,从右往左,找到的是 28,8541已经是所能构成的最大的了,所以要对更高位的2进行操作,将2变大。
由于要从小到大排列,所以i-1位置需要尽可能小地变大,所以将i-1位置与i及右边元素中刚刚大于i-1元素的元素j位置进行交换,实现稍稍增大i-1位置。上面例子就是2和4交换,变成 348521.
交换增大之后,我们需要将i-1的右边的这些元素,变成从小到大排列。这里无需做一遍排序,想想刚才找到的j位置,其元素是刚好大于i-1位置的,那么将i-1和它交换之后,此位置的元素仍然是 小于 j-1,大于j+1的,也就是说,i-1右边的这个序列,仍然是倒序有序的,例如上面 348521. 只需要将这个序列反转一下,就实现了从小到大排序。
下面放一张来自 Leetcode 官方题解的动图,以便理解:

# 代码
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
i = len(nums) - 1
while i > 0 and nums[i-1] >= nums[i]: # 从右向左找,找到第一个 i-1比i位置元素小的
i -= 1
if i > 0: # 找到了 (如果没找到,说明已经是逆序了,此时i=0,没关系,正好此时将整个数组做一次反转,就是从头开始的最小排列)
j = len(nums) - 1
while j >= 0 and nums[j] <= nums[i-1]: # 在右边从右向左找,找到可以和i-1交换的j
j -= 1
nums[i-1], nums[j] = nums[j], nums[i-1] # 交换
nums[i:] = nums[i:][::-1] # 将i及i右边的这部分做反转。python真方便啊
2
3
4
5
6
7
8
9
10
11
12
13
14