 Leetcode题解(12)- 2018 力扣 Leetcode CN 高频题汇总 part 8
Leetcode题解(12)- 2018 力扣 Leetcode CN 高频题汇总 part 8
# 快乐数
Leetcode 202 题
# 问题
编写一个算法来判断一个数是不是“快乐数”。
一个“快乐数”定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1。如果可以变为 1,那么这个数就是快乐数。
示例:
输入: 19
输出: true
解释:
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1
2
3
4
5
6
7
8
9
# 思路
按题目要求来循环计算快乐数吧,同时把之前的结果存下来,当发现有重复出现的数字时,说明不是快乐数,出现无限循环了。
# 代码
class Solution(object):
def isHappy(self, n):
already = set()
while n != 1:
num = 0
while n > 0:
tmp = n % 10
num += tmp**2
n //= 10
if num in already:
return False
else:
already.add(num)
n = num
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 两整数之和
Leetcode 371题
# 问题
不使用运算符 + 和 - ,计算两整数a b之和。
# 思路
那就位运算吧。位运算的 xor 相当于做了无进位的加法,比如说 0101 和 0100 做xor后得到 0001。而与运算相当于做了加法的进位,例如 0101 和 0100 做与运算后得到 0100 需要再左移一位变成 1000 这就是加法的进位。
按说接下来把 0001 和1000 相加就完成了,但是不能用加法,那其实目前就是把原来 0101 和 0100 的加法,转换成了 0001 和 1000 的加法了。所以继续重复 xor 和 与 运算,直到进位变成0,这时意味着不再需要进位了, 得到的无进位值就是最终结果。
# 代码
python中的特殊处理 在 Python 中,整数不是 32 位的,也就是说你一直循环左移并不会存在溢出的现象,这就需要我们手动对 Python 中的整数进行处理,手动模拟 32 位 INT 整型。
具体做法是将整数对 0x100000000 取模,保证该数从 32 位开始到最高位都是 0。
class Solution(object):
def getSum(self, a, b):
"""
:type a: int
:type b: int
:rtype: int
"""
# 2^32
MASK = 0x100000000
# 整型最大值
MAX_INT = 0x7FFFFFFF
MIN_INT = MAX_INT + 1
while b != 0:
# 计算进位
carry = (a & b) << 1
# 取余范围限制在 [0, 2^32-1] 范围内
a = (a ^ b) % MASK
b = carry % MASK
return a if a <= MAX_INT else ~((a % MIN_INT) ^ MAX_INT)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
感觉python不适合搞二进制 hhhhhh
# Fizz Buzz
Leetcode 412题
# 问题
写一个程序,输出从 1 到 n 数字的字符串表示。
- 如果 n 是3的倍数,输出“Fizz”;
- 如果 n 是5的倍数,输出“Buzz”; 3.如果 n 同时是3和5的倍数,输出 “FizzBuzz”。
示例:
n = 15,
返回:
[
"1",
"2",
"Fizz",
"4",
"Buzz",
"Fizz",
"7",
"8",
"Fizz",
"Buzz",
"11",
"Fizz",
"13",
"14",
"FizzBuzz"
]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 代码
class Solution(object):
def fizzBuzz(self, n):
ret = []
for i in range(1, n+1):
fizz = i % 3 == 0
buzz = i % 5 == 0
if fizz and buzz:
ret.append('FizzBuzz')
elif fizz:
ret.append('Fizz')
elif buzz:
ret.append('Buzz')
else:
ret.append(str(i))
return ret
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 加油站
Leetcode 134题
# 问题
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明: 如果题目有解,该答案即为唯一答案。 输入数组均为非空数组,且长度相同。 输入数组中的元素均为非负数。
示例 1:
输入:
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入:
gas = [2,3,4]
cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 思路
首先可以明确,如果 sum(gas) 比 sum(cost) 小,那肯定是不能完成的,如果大于等于的话,则是一定可以完成的.
所以开始遍历,用total来累计gas和cost,最后如果total小于0说明不能完成;用tank表示当前油箱的油,如果在某个点tank小于0了,则tank重置为0并标记这个点为起始点,用 gas[i]-cost[i] 来更新tank。
# 代码
class Solution(object):
def canCompleteCircuit(self, gas, cost):
tank, total = 0, 0
start = 0
for i in range(len(gas)):
total += gas[i] - cost[i]
if tank < 0:
tank = gas[i] - cost[i]
start = i
else:
tank += gas[i] - cost[i]
return start if total >= 0 else -1
2
3
4
5
6
7
8
9
10
11
12
# LRU 缓存机制
leetcode 146题
# 问题
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
获取数据 get(key) - 如果密钥 (key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在,则写入其数据值。当缓存容量达到上限时,它应该在写入新数据之前删除最近最少使用的数据值,从而为新的数据值留出空间。
你是否可以在 O(1) 时间复杂度内完成这两种操作?
示例:
LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得密钥 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得密钥 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4
2
3
4
5
6
7
8
9
10
11
12
# 思路
所使用的数据结构如下图所示:
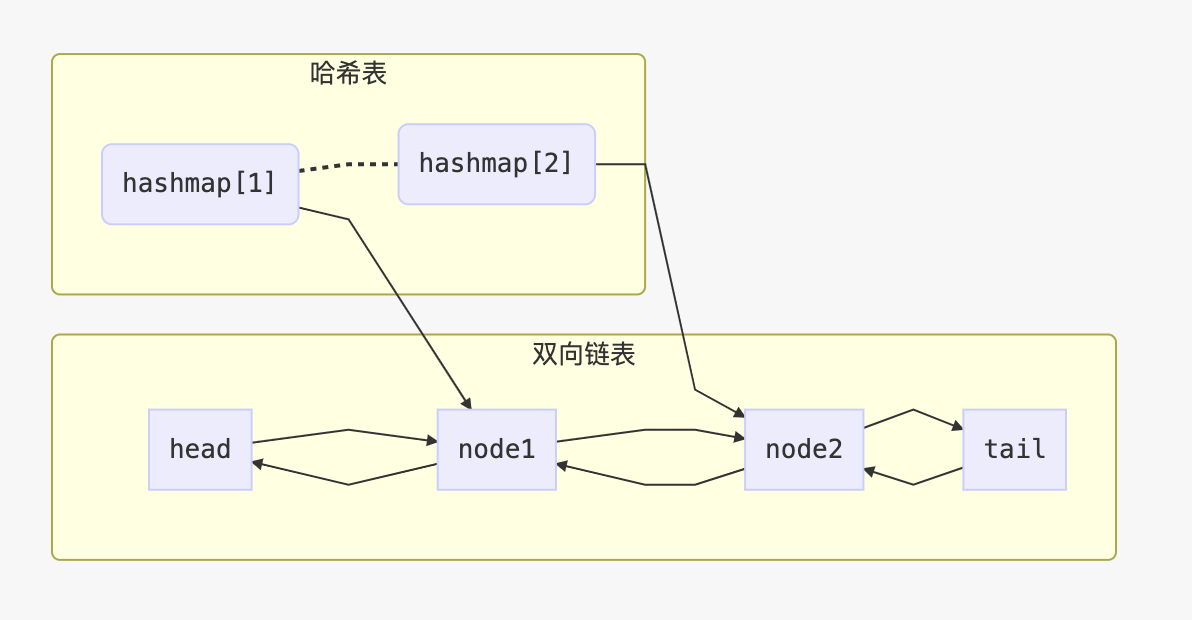
使用哈希表来进行 k v 的访问,实现快速的get操作。通过双向链表及指针操作,快速实现将某个最近访问过的节点,移动到链表尾部。
具体参照下面的代码。最重要的就是要知道LRU可以用这种数据结构来实现,这样可以O(1)的来完成查找和插入操作。具体的则是代码实现时的一些细节要注意,包括链表改指针的先后顺序啦等等。
# 代码
class ListNode(object):
def __init__(self, key=None, value=None):
self.key = key
self.value = value
self.prev = None
self.next = None
class LRUCache(object):
def __init__(self, capacity):
self.capacity = capacity
self.hashmap = {}
# 空的头尾节点
self.head = ListNode()
self.tail = ListNode()
self.head.next = self.tail
self.tail.prev = self.head
# 将给定key的节点移动到尾部
def move_to_tail(self, key):
# 获取节点
node = self.hashmap[key]
# 将节点从原来位置删除
node.prev.next = node.next
node.next.prev = node.prev
# 将节点追加到空的tail节点之前
node.prev = self.tail.prev
node.next = self.tail
self.tail.prev.next = node
self.tail.prev = node
def get(self, key):
# 节点存在,则读取,并移至末尾表示最近更新过
if key in self.hashmap:
self.move_to_tail(key)
node = self.hashmap.get(key, None)
if node:
return node.value
else:
return -1
def put(self, key, value):
# 节点存在
if key in self.hashmap:
# 需要注意,值可能会更新
self.hashmap[key].value = value
# 移至末尾,表示最近更新过
self.move_to_tail(key)
else:
# 容量超限
if len(self.hashmap) == self.capacity:
# 删除头部的节点
self.hashmap.pop(self.head.next.key)
self.head.next = self.head.next.next
self.head.next.prev = self.head
# 新建节点
new = ListNode(key, value)
self.hashmap[key] = new
# 新节点放在尾部
new.prev = self.tail.prev
new.next = self.tail
self.tail.prev.next = new
self.tail.prev = new
# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
太棒啦~ 力扣 2018 高频题这个专题,终于完成啦~~ 完结撒花!
接下来做一下力扣里的 热题 100 、 精选 TOP 面试题 、腾讯50题 这几个专题吧,当然很多题目是已经做过了的就不再重复刷。看上去大概还需要再做六七十题的样子。