根据从网上看的一些博文，简单整理下我的理解。

我们有一堆数据（X，y）， X特征，y表示类别标签。那么目的是希望能够计算出 p(y|X)。

判别式模型直接对 p(y|X) 进行建模，也就是说将来给了新的X，直接就能计算出这个概率。

生成式模型则对 p(X, Y) 建模，根据贝叶斯公式可以计算出 p(y|X) 。

生成式模型可以更多地体现出数据本身的信息，且根据生成式模型可以得到判别式模型，反之则不能。

举个例子： 现在有4个样本数据，(1,0), (1,0), (2,0), (2,1)

如果使用生成式模型，我们对 p(X, Y) 建模，可以得到下表：

	y=0	y=1
x=1	1/2	0
x=2	1/4	1/4

整个表格的数字加起来为1.

如果是判别式模型，对 p(y|X) 建模，可以得到下表：

	y=0	y=1
x=1	1	0
x=2	1/2	1/2

表格中，给定x，每一行的值和为1。

根据联合概率表和贝叶斯公式，是可以计算出条件概率表的。

p(y=0|x=1) = p(x=1, y=0) / p(x=1) = (1/2) / (1/2) = 1

p(y=0|x=2) = p(x=2, y=0) / p(x=2) = (1/4) / (1/2) = 1/2

搬运一张对比表：

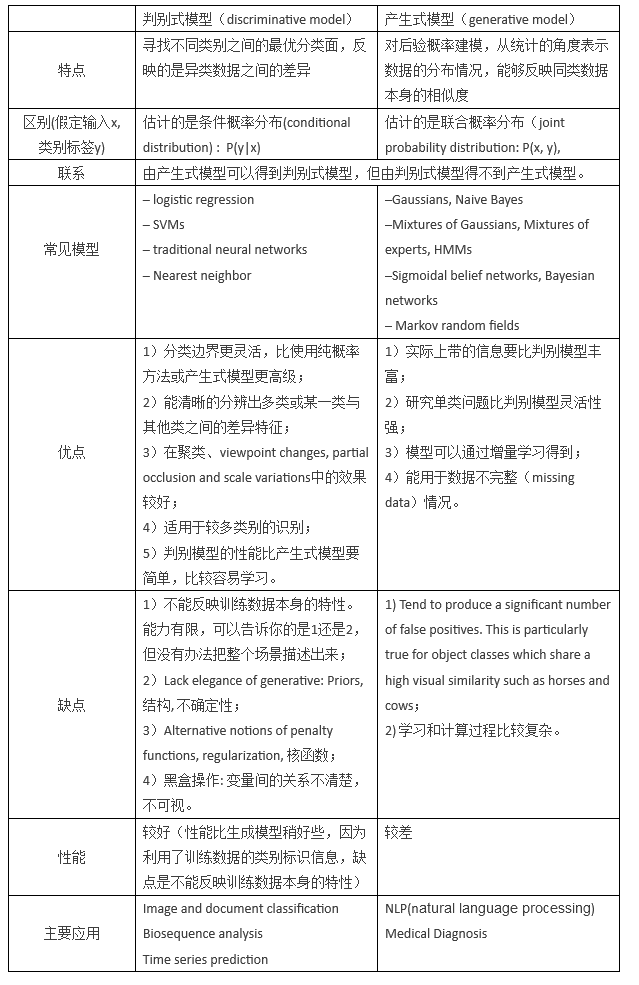
（以下来自统计学习方法）

生成方法的特点：生成方法可以还原出联合概率分布P(X,Y)，而判别方法则不能；生成方法的学习收敛速度更快，当样本容量增加的时候，学到的模型可以更快地收敛于真实模型；当存在隐变量时，仍可以用生成方法学习，此时判别方法就不能用。

判别方法的特点：判别方法直接学习的是条件概率P(Y|X)或者决策函数f(X)，直接面对预测，往往学习的准确率更高；由于直接学习P(Y|X)或者f(X)，可以对数据进行各种程度上的抽象、定义特征并使用特征，因此可以简化学习问题。