更新：此题解 markdown 源文件已放到 Github https://github.com/bytetopia/offer-coding-interviews-python (opens new window)，欢迎前去给个小星星鸭！

---

知识点：二叉树、栈和队列、查找

二叉树

知识点

• 树的概念：分支节点、叶节点、度、深度……
• 二叉树的定义，满二叉树，完全二叉树
• 二叉树的五条性质
• 二叉树的存储方式（二叉链表广泛采用）
• 二叉树的遍历（前序、中序、后序）（递归、非递归），以及层次遍历（采用队列）

题目：重建二叉树

要求

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

思路

前序序列能确定根节点，用根节点，把中序划分为左右子树 基于递归的思路，重复上述步骤

代码

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回构造的TreeNode根节点
    def reConstructBinaryTree(self, pre, tin):
        # 给定前序和中序，重建二叉树
        # 思路：前序结果可以确定树根，通过树根可以将中序切成左右两半
        if(len(pre)==0):
            return None
        root = TreeNode(pre[0])
        tin_root_index = tin.index(root.val)
        if tin_root_index > 0:  # 有左子树
            new_tin = tin[0: tin_root_index]
            new_pre = pre[1: len(new_tin)+1]
            root.left = self.reConstructBinaryTree(new_pre, new_tin)
        if tin_root_index != len(tin) - 1:  # 有右子树
            new_tin = tin[tin_root_index+1:]
            new_pre = pre[len(pre)-len(new_tin):]
            root.right = self.reConstructBinaryTree(new_pre, new_tin)
        return root

这个题主要是清楚前序和中序的特点，理清思路以后，算准确切分的下标，递归实现就行。 下标可以写的更简洁一点：

        index = tin.index(root.val)
        if index > 0:  # 有左子树
            root.left = self.reConstructBinaryTree(pre[1: index+1], tin[0: index])
        if index != len(tin) - 1:  # 有右子树
            root.right = self.reConstructBinaryTree(pre[index+1: ], tin[index+1: ])
        return root

栈和队列

题目：用两个栈模拟队列

要求

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

思路

一个栈处理push，新节点放入该栈，一个栈处理pop，初始为空 当需要pop时，如果pop栈不空，则直接出栈，如果空，则从push栈弹出全部内容放到pop栈，pop栈出栈一个

代码

# -*- coding:utf-8 -*-
class Solution:
    # 思路：
    # 一个栈处理push，新节点放入该栈，一个栈处理pop，初始为空
    # 当需要pop时，如果pop栈不空，则直接出栈，如果空，则从push栈弹出全部内容放到pop栈，pop栈出栈一个
    
    def __init__(self):
        self.push_s = []
        self.pop_s = []
    
    def push(self, node):
        # write code here
        self.push_s.append(node)
     
    def pop(self):
        # return xx
        if len(self.pop_s) == 0:
            if len(self.push_s) == 0:
                return None
            for i in range(0, len(self.push_s)):
                self.pop_s.append(self.push_s.pop(-1))
        return self.pop_s.pop(-1)

思路很简单，主要是实现的时候，下标不要写越界。

今天看到一个题，说用两个栈（长度分别为m、n，m大于n）来模拟队列，最大容量是多少。答案是 2n+1， 可以参考 https://www.cnblogs.com/eniac12/p/4865158.html

扩展

如果用两个队列来模拟栈呢？

做法是用两个队列交替使用，一个存数字一个始终为空。如果入栈则存数字的队列继续往后入队；如果要出栈的话，则在有数字的队列进行一次倒腾，依次出队并写入原本为空的队列，只留下最后一个元素弹出。两个队列交替着用。

查找

题目：旋转数组的最小数字

要求

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

思路

简单直接的思路：从前往后扫，找到第一个比上一个元素小的元素，就说明是最小元素了。 【注意特例】整个数组未旋转

代码

class Solution:
    def minNumberInRotateArray(self, rotateArray):
        # 思路
        # 数组应该为非递减，找到第一个比上一个元素小的位置，就是最小值
        if len(rotateArray) == 0:
            return 0
        for i in range(len(rotateArray)-1):
            if rotateArray[i+1] < rotateArray[i]:
                return rotateArray[i+1]
        # 都没找到
        return rotateArray[0]

感觉写完一遍跑过美滋滋，然而这种方法的时间复杂度为O(n)。

鉴于旋转数组前后两半都是有序的，可以采用类似二分查找的方法，减少比较次数。

思路2

如果用二分的话，整个思路会比较复杂一些，核心是通过比较 mid 位置和 low/high 位置的元素大小，判断这个旋转点位于前半段还是后半段，然后调整 low或者high，缩小范围，直到最终 low和high位置重合，找到最小点。

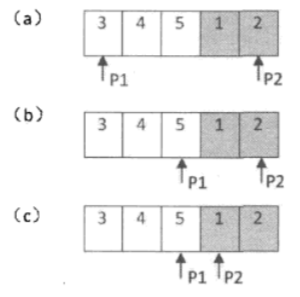
具体思路需要理一下，可以参考这两篇文章详细

https://blog.nowcoder.net/n/dcb0f2e6ffd44e1895b7a5297e362778?f=comment (opens new window)

和 https://blog.nowcoder.net/n/1e5cd58cbd0c4c3b855b635c1230469c?f=comment (opens new window)

另外尤其需要注意的一点是 ，题目中只说非递减，但没有说递增，所以是可能会存在连续几个相等的数字的。

代码2

class Solution:
    def minNumberInRotateArray(self, rotateArray):
        # write code here
        if rotateArray is None or len(rotateArray) == 0:
            return 0
        low = 0
        high = len(rotateArray) - 1
        arr = rotateArray
        while(low < high):
            if arr[low] < arr[high]: # 说明这段未旋转，直接退出
                return arr[low]
            mid = (low+high)//2
            if arr[mid] < arr[low]: # 说明low< x <=mid肯定包含了最小点 （实际发现 mid跟low或者high比好像都行，总之就是一种是high往前缩，一种是low往后进）
                high = mid
            elif arr[mid] > arr[high]:  # 说明mid < x <= high肯定包含了最小点，且mid处肯定不是最小点
                low = mid +1
            else:  # 说明high 和 low相等了，此时low处不是数组最小点，low++继续找 （实际发现high--也能行）
                low += 1
        return arr[low]
    

这个题还是有点绕的，看到了几个不同风格的代码，牛客用例都能跑过，时间有限这次难以深究。如果发现哪里有问题欢迎评论区留言指出，感谢。