检索技术是更底层的通用技术，它研究的是如何讲我们所需要的数据高效地取出来。

• 基础技术篇主要包括常见且核心的数据结构和检索算法
• 进阶实战篇主要结合工业界的应用场景，深入介绍一些高级检索技术和架构设计思想
• 系统案例篇对当前热门的应用方向进行分析

---

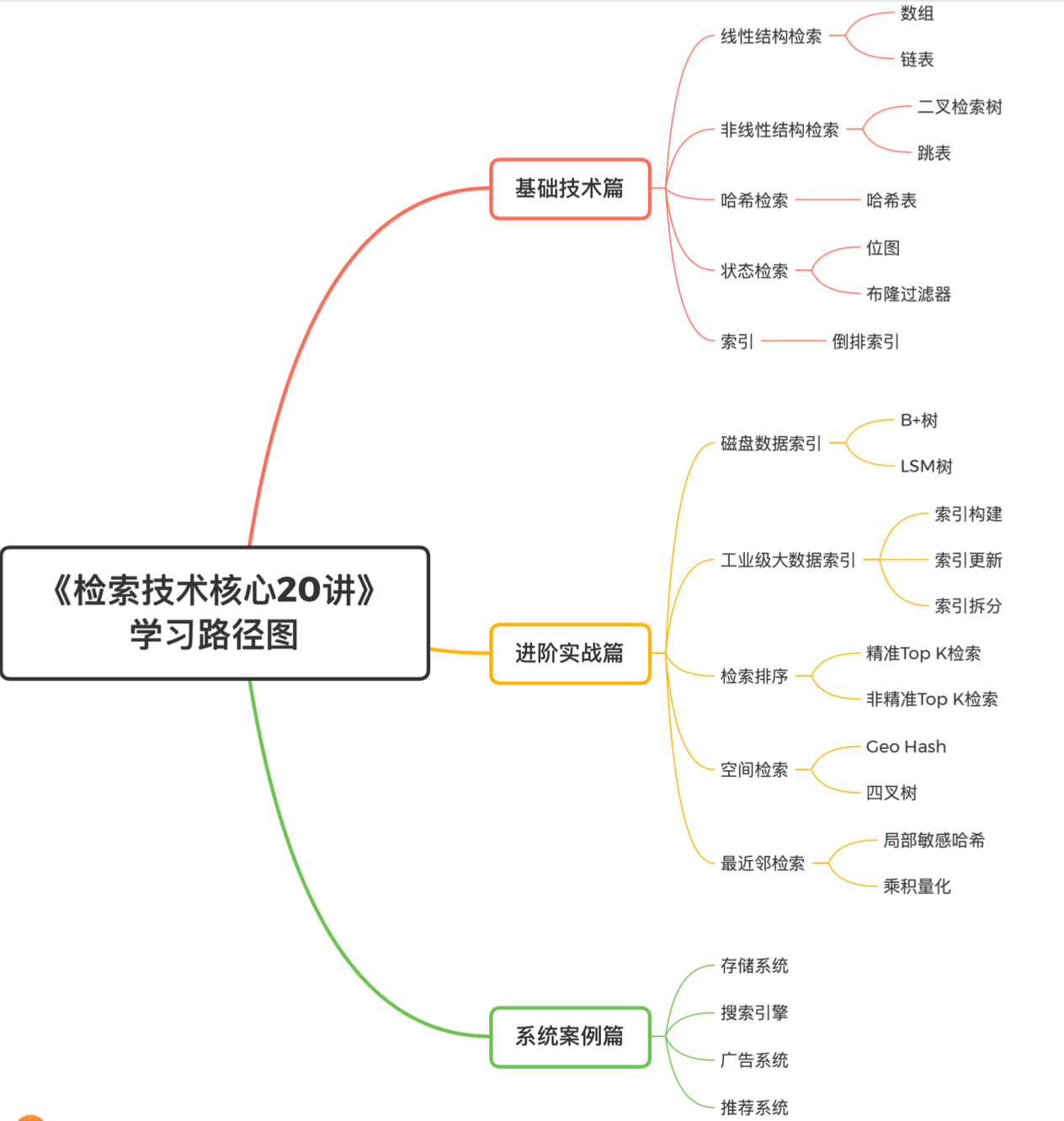
1. 磁盘数据索引：数据库检索 B+树

将数据与索引分离：内存访问速度快，但存储成本高，磁盘访问慢，对磁盘的访问次数应该尽可能的少。

• B+树可以将树形索引的所有节点都存在磁盘上，而不必存在内存，适合大索引。其中一个关键设计是，让一个节点的大小等于一个块的大小，节点存储的数据不是一个元素，而是一个可以装m个元素的有序数组。这样可以提高读取效率。

• 另一个设计是节点分为内部节点和叶子节点，内部节点只存储key和指针，叶子节点存储key和数据。

B+树还将同一层的所有节点组成了有序的双向链表，这样就同时具备了良好的范围查询能力和灵活调整的能力。

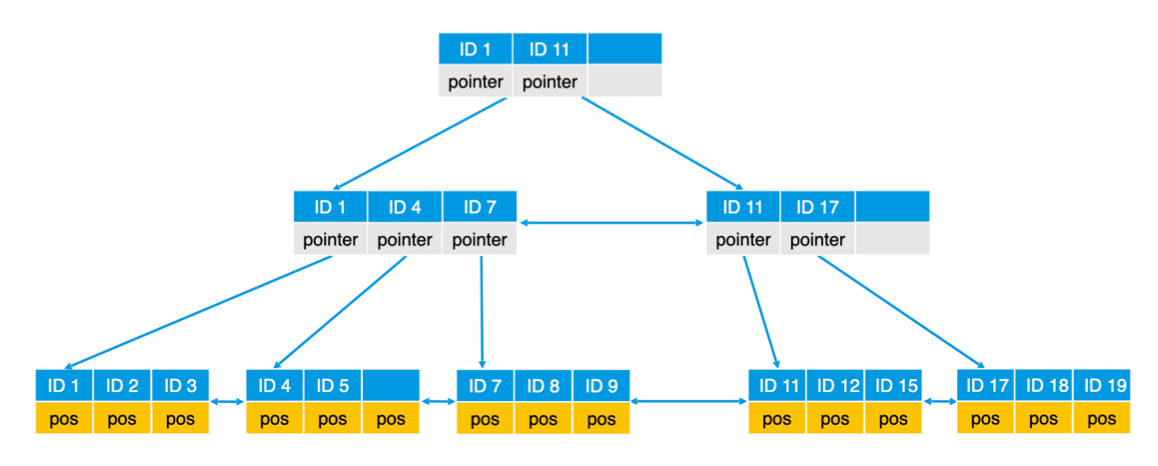
• 检索时，逐层访问直到读到叶子节点。B+树的层数往往很矮，但可以索引数量很大的数据。

• B+树的调整：插入元素时，如果叶子节点满了，则进行分裂，相应的上层内部节点也要调整；删除元素同理，如果过于空闲，则要进行合并。

• B+树并不比有序数组或者二叉搜索树的检索效率更高，但最大的优点在于，可以将索引数据存储在磁盘中并高效检索。

2. 磁盘数据索引：日志系统 LSM 树

日志系统会持续大量生成和写入记录，检索时往往更倾向于对近期数据做检索。可以使用 LSM 树（Log structured merge trees）。

• 批量写入：数据延迟写磁盘。LSM树至少有两棵，一棵C0树在内存中，较小，另一棵C1在磁盘，较大。数据新来时先写入C0树，C0满了之后才会和C1合并写入磁盘。C1树可以将所有叶子节点都写满，因为它不需要支持随机单条记录的写入了。

• 崩溃恢复机制：对C0数据的修改会写log文件，记录检查点，当断电后可以根据log恢复内存数据。

• 合并C0和C1的优化：节点尽可能存放到连续的块中。

• 检索：先找C0，再找C1。

• 删除数据：延迟写入的思路，可以先在C0中置删除标记。

3. 工业级大数据索引：索引构建

倒排索引的key是词的id和词的文本，内容是文档的id，也会记录该词在文档中出现的次数和位置等信息。

• 构建倒排索引

  • 将文档划分为多个小的集合
  • 在内存中生成倒排，存入磁盘，按照关键词的字符串进行排序
  • 将磁盘中的多路倒排进行归并

• 检索

  • 词典可能会比较大，可以用B+树来存储和检索词典
  • 通过词典找到关键词对应的posting list，读取并处理
  • 长度过大的posting list无法一次读入内存，可以也建立索引或者分层跳表处理
  • 也可以借助LRU缓存，将频繁使用的posting list缓存起来，减少磁盘IO

优化思想：一个是索引压缩，可以对词典进行压缩（比如通过前缀树）使之能够加载到内存；一个是将大数据集拆成小的来处理。

4. 工业级大数据索引：索引更新

• 内存更新：双缓冲机制，保存两份索引，读取用A，要更新时只更新B，当积累一批更新后，将主索引切换到B。

• 全量更新：磁盘全量和内存增量结合。

  • 可以将新收到的数据存在内存中，作为增量；
  • 查询时增量和磁盘全量结合查询；
  • 另外维护一个删除列表（由于删除一个文档会引起大量倒排更新，所以这里不要直接置删除标记，而是另外存一个删除列表，检索结果排除掉该列表中的内容，往往更高效些）；

• 如何将增量和全量索引合并？

  • 完全重建：适合索引量小
  • 归并合并
  • 滚动合并：如果全量很大，增量很小，归并合并效率很低，因为为了更新少量增量，要读取大量全量索引。可以用滚动合并法，也就是按时间周期分层建大索引，比如天级、周级、全量等。合并时，先把增量合并到天级，以此类推。这样的话， 要很久才能轮到一次大索引的全量合并。

5. 工业级大数据索引：索引拆分

实现一个分布式的检索系统。

• 按业务拆分。比如图书分成国内国外，搜索时用户可以选择，这样只查指定业务的索引。

• 按文档拆分。每个机器包含全部关键词，但倒排里只包含部分文档。可以提高单台机器的检索效率，但是每次都需要请求所有机器，所以分片不宜过多。

• 按关键词拆分。每台机器上的词典不完整，但文档列表是完整的。会存在部分机器负载过大（热点词访问量高，而且高频词倒排列表很长）的问题。

通常还是按文档拆分更多一些？比如，当新文档加入时，按文档拆分可以只增加在新机器上，但是按关键词拆分则需要把涉及的关键词每台机器都更新。

6. 检索排序：精准 top K

打分的方式

1） TF-IDF

TF-IDF 的计算 （加log做平滑处理，为避免分母为0， df需要+1）

TF = 1 + log(tf)

IDF = log (N / (df+1))

那么，一个词项t在文档d的权重，就可以通过 TF x IDF 算出。一条查询中会有多个词项，把每个词项和文档的相关性累加，就可以算出这条查询q和文档d的相关性得分。

2）BM25算法

具体公式不写了，是一种相对更复杂的计算方式，考虑了四个因子：IDF、文档长度、文档中的词频、查询词中的词频。并且，有三个可以人工调整大小的参数，用来调节词频、文档长度等因子在打分中的重要性。

3）机器学习进行打分

快速进行 Top K

可以使用堆排序代替全排序，只要取得分最高的前 K 个就行了。排序的代价从 nlogn 降到了 n(建堆) + klogn （堆排）。由于 k往往远小于n，带来的提升还是很可观的。

7. 检索排序：非精准 top K

不一定全部算，全部排，精准计算 top K。只要保证质量够高的结果，能包含在 top K 里，满足用户所需就行了。可以节省成本和计算量。

分成两个阶段：召回和排序。召回阶段可以用非精准，做个初筛，大幅降低召回的文档量，排序阶段再使用打分机制做精准 top K。

• 静态质量得分阶段：按照文档的静态质量分，对关键词的posting list进行降序排序，并截断。打分仅和结果本身的质量有关，比如网页的 page rank。

• 根据词频：可以根据词频和静态质量分综合考虑，对某个关键词的倒排列表进行截断。不过有风险，比如某个文档同时包含ab两个关键词，但由于其得分低，均未在两个关键词的倒排中，但实际上这个文档跟检索的相关性是比较高的，会造成结果的丢失。

• 使用分层索引。建立高质量和低质量索引，先取高质量，如果足够k个就够了，不够k个再去低质量里取。

为了保证结果的多样性，也可以采用 exploit and explore，即小比例返回一些得分不那么高的结果，给他们一些证明自己的机会。

8. 空间检索：geohash

可以通过限定附近检索的范围，对空间进行划分，并进行编号，实现查找附近的人。

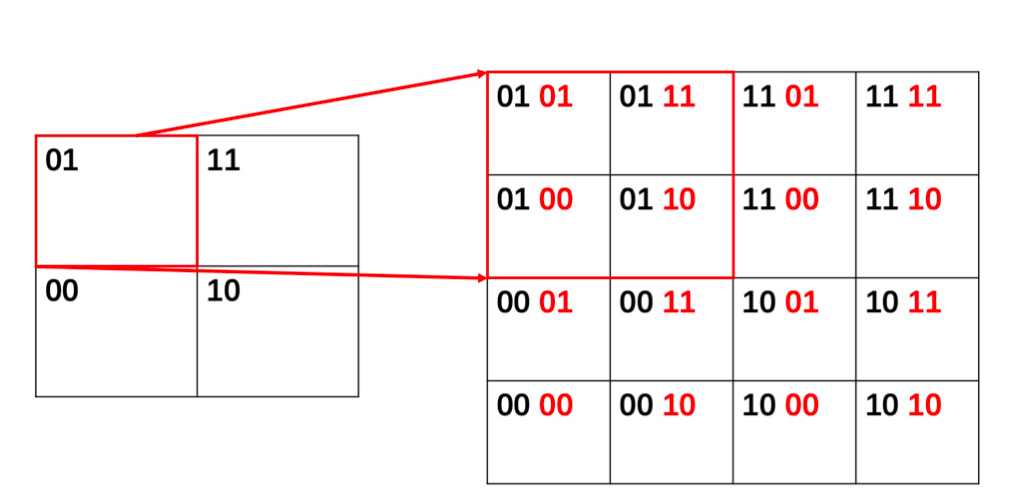
这种编号的好处：

• 区域有层次关系，前缀相同说明属于同一个大区域
• 编码有分割意义，奇数位代表垂直切分，偶数位代表水平切分，便于进行上下左右查找计算。

如何快速查询附近的人： 通过区域编码，可以找到一定层级上与当前区域邻接的区域，查找里面的用户就行。如果数量不够，还可以继续扩大范围查找。

什么是 geohash：

1）将经纬度进行切分，比如纬度上，每次切分上半边记为1，下半边记为0，那么比如39，在纬度的0-90属于上半边，第一位就是1，0-90再次切分，它属于0-45，属于下半边，记为0，所以两位编码就是 10。以此类推。最后获得区域的编码。

2）将二进制编码简化表示，可以以5个bit为一个单位，转化为base32编码（因为2^5=32)，更直观。

不同位数的编码可以代表不同的切分粒度，位数越长，切分粒度越细。

9. 空间检索：四叉树

在第8小节中提到检索附近的人，数量不够就扩大范围。由于 geohash 是可以排序的，扩大范围时，我们就需要从头二分来找到合适的位置。

由于我们每次切分都是按照水平和垂直，切出 01，10，11，00 四种结果，所以可以借助四叉树的结构，来存储这个切分的过程。这样的话，如果当前区域找不到，我们就到上一层，以这一层的区域进行检索，避免了从头进行二分查找。

10. 最近邻检索：局部敏感哈希 LSH

一个应用：对相似文章去重。这些文章可能内容很相似，但是不是完全每个字符一模一样。

局部敏感哈希

我们对空间进行多次切分，如果两个点多次切分后都在同一边，那说明他们很大概率上是相近的。所以在高维空间，随机生成n个超平面，每个都把空间分成两份，在上代表1在下代表0，获得n位的序列，如果两个点的序列的海明距离（比特位差异）较小，则说明这两个点位置很近。

SimHash

思路类似LSH，但是做了优化。首先是只使用一个哈希函数，而且不是对整个文档做哈希，而是对每个关键词做哈希。关键词也是有不同权重的，有的重要有的次要。

1）获得一个哈希函数 2）给每个关键词生成哈希值，并且把二进制中的0改成-1 3）哈希值乘上关键词自己的权重，比如权重为2，则原来的(-1,1,1)就变成了(-2,2,2) 4）文档所有关键词的编码按位相加 5）结果里面大于0的记为1，小于0的记为0，这样最后的编码还是二进制。

SimHash的好处，一个是就用了一个哈希函数，比超平面划分更简单；更重要的是通过乘以权重，体现了关键词重要性的差异，权重高的关键词更容易影响最终的结果。

抽屉原理进行相似检索

获得simHash值之后，怎么找相似的文档呢？一个一个对比效率很低。

这里有一个抽屉原理：比如3个球放到4个抽屉，必有一个是空的。那么假设我们容忍的海明距离是3，也就是说3个bit及以内的差异，就认为是相似。那么，可以把Simhash切成四段，那如果一个文档要跟我们的目标文档相似的话，最多只能有3bit的差异，也就是肯定会有一段的值完全相同。那么按照这个条件，就可以快速召回一批文档了。

具体可以对每段切分后，按值构建倒排，这样可以从倒排里快速取文档。

SimHash的缺点？处理的更多的是字面上的相似而非语义相似。

11. 最近邻检索：乘积量化

聚类

SimHash是一个非精确的方案。我们可以把文本、图片表示成含有语义的向量。怎么计算向量的相似呢？可以用聚类算法，例如 K-Means。

聚类之后，可以用每个聚簇的 ID 作为key，建立倒排。新的向量来了之后，先计算和每个类中心的距离，找邻近的，然后拿着类的ID取倒排里面查元素就可以了。节点很多时，也可以用层次聚类，分层查询。

乘积量化压缩空间

将向量的高维空间看成多个子空间的乘积，然后对每个子空间，用聚类技术分成多个区域，给每个区域编码。实现将向量压缩。

比如我们把向量切成4段，每段的取值进行聚类，从而实现将这段的很多个取值压缩成很少个类。每个类我们存下中心向量，这个类里的向量都以它的中心向量为表示，不存各自的值了。从而实现压缩。

当计算相似性时，我们对新的查询向量也采用类似的切分，每段去跟这段的各个聚类中心算距离。

这样，也可以用聚类中心的ID去建倒排，优化查询速度。