 算法与数据结构 | 二叉搜索树
算法与数据结构 | 二叉搜索树
# 二叉搜索树
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是-指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
二叉搜索树在查找当中用途非常广泛。
# 二分查找法
对于有序数组,才能使用二分查找法。时间复杂度 O(logn)
def binary_search(arr, target):
# return the index of target or -1 if target is not found
# 在 [l...r] 之间查找target
l = 0
r = len(arr) - 1
while l <= r:
# mid = (l + r) // 2 # 潜在bug:整数溢出
mid = l + (r - l) // 2
if arr[mid] == target:
return mid
if target < arr[mid]:
r = mid - 1
else:
l = mid + 1
return -1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
arr = [1, 3, 4, 5, 6, 7, 8, 10, 12]
binary_search(arr, 2)
1
2
2
-1
# 二叉搜索树
堆一定是完全二叉树,而二叉搜索树未必是完全二叉树,所以堆可以用数组结构来存储,而二叉搜索树就要用树来存储。
下面代码定义了二叉搜索树的结构,并实现了 插入、查找、深度优先遍历、广度优先遍历、删除节点(删除最大值、最小值、任意节点) 等操作。
class Node(object):
def __init__(self, key, value):
self.key = key
self.value = value
self.left = None
self.right = None
class BST(object):
def __init__(self):
self.root = None
self.count = 0
def size(self):
return self.count
def is_empty(self):
return self.count == 0
def insert(self, key, value):
self.root = self._insert(self.root, key, value)
def _insert(self, node, key, value):
# 递归调用,向以node为根的树中,插入键和值分别为key和value的节点。返回插入新节点后这棵树的根。
if node == None:
self.count += 1
return Node(key, value)
if key == node.key:
# 一般二叉搜索树中不应有重复的key值。如果插入的key值已存在,则以新的value覆盖旧的value
node.value = value
elif key < node.key:
node.left = self._insert(node.left, key, value)
else: # key > node.key
node.right = self._insert(node.right, key, value)
return node
def search(self, key):
return self._search(self.root, key)
def contain(self, key):
return self._search(self.root, key) != None
def _search(self, root, key):
# 递归调用,按key查找节点,返回节点的value
if not root:
return None
if root.key == key:
return root.value
elif key < root.key:
return self._search(root.left, key)
else:
return self._search(root.right, key)
def pre_order_visit(self):
self._per_order_visit(self.root)
def _pre_order_visit(self, node):
# 递归调用,前序遍历
if node:
print(node.key)
self._pre_order_visit(node.left)
self._pre_order_visit(node.right)
def mid_order_visit(self):
self._mid_order_visit(self.root)
def _mid_order_visit(self, node):
# 递归调用,中序遍历
if node:
self._mid_order_visit(node.left)
print(node.key)
self._mid_order_visit(node.right)
def post_order_visit(self):
self._post_order_visit(self.root)
def _post_order_visit(self, node):
# 递归调用,后序遍历
if node:
self._post_order_visit(node.left)
self._post_order_visit(node.right)
print(node.key)
def level_order_visit(self):
# 借助队列实现层序遍历
q = []
q.append(self.root)
while len(q) != 0:
node = q[0]
q.pop(0)
print(node.key)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
def minimum(self):
if not root:
return None
min_node = self._minimum(self.root)
return min_node.key
def _minimum(self, node):
# 递归查找最小值。其实就是一直向左下方寻找,最左下的就是最小值
if not node.left:
return node
return self._minimum(node.left)
def maximum(self):
if not root:
return None
max_node = self._maximum(self.root)
return max_node.key
def _maximum(self, node):
# 递归查找最大值。其实就是一直向右下方寻找,最右下的就是最大值
if not node.right:
return node
return self._maximum(node.right)
def remove_min(self):
# 删除最小值。最小值节点肯定没有左孩子,如果也没有右孩子,那直接删掉即可。如果有右孩子,则将其作为最小值节点的父节点的左孩子。
if self.root:
self.root = self._remove_min(self.root)
def _remove_min(self, node):
# 删除以node为根的子树中的最小节点,并返回新的这棵子树的根
if not node.left: # 是最小节点了
right = node.right # 一句话即涵盖了两种情况:有右孩子则将右孩子作为新根,没有右孩子则将None作为新根
del node
self.count -= 1
return right
# 不是最小节点,继续往左下方寻找
node.left = self._remove_min(node.left)
return node
def remove_max(self):
# 删除最大值。最大值节点肯定没有右孩子。如果也没有左孩子,直接删掉;如果有左孩子则将左孩子作为该最大值节点的父节点的右孩子即可。
if self.root:
self.root = self._remove_max(self.root)
def _remove_max(self, node):
# 删除以node为根的子树中的最小节点,并返回新的这棵子树的根
if not node.right: # 是最大节点了
left = node.left
del node
self.count -= 1
return left
# 不是最大节点,继续往右下方寻找
node.right = self._remove_max(node.right)
return node
def remove(self, key):
# 删除任意节点
# 如果节点只有左子树或者右子树,可以按照上面 删除最大值和最小值的方法,直接顶位即可。
# 如果左右都有,则比较复杂,按照二叉搜索树的性质,当前节点值大于左子树,且小于右子树,所以应当用右子树中的最小值节点来顶位。
# 具体操作:
#(1)要删的节点为d
#(2)找到d的右子树的最小节点s,用于顶替d,另存为节点n
#(3)按照之前remove_min的方法,把d的右子树中的最小节点s删除掉
#(4)remove_min方法会返回删除了最小节点s之后的右子树的新的根,作为n的右子树
#(5)n的左子树,就是原d的左子树
#(6)删除d,n是新的根,返回回去,完成删除
# 可以画图辅助理解
self.root = self._remove(self.root, key)
def _remove(self, node, key):
# 递归,从当前node为根的子树中删除key,并返回删除之后的新的根
if not node:
return None
if key < node.key:
node.left = self._remove(node.left, key)
return node
elif key > node.key:
node.right = self._remove(node.right, key)
return node
else: # key == node.key
if not node.left: # 只有右孩子,或者左右都为空,直接删
right = node.right
del node
self.count -= 1
return right
if not node.right: # 只有左孩子,直接删
left = node.left
del node
self.count -= 1
return left
# 左右两孩子都有
s = self._minimum(node.right) # 找到右子树的最小值,作为替补节点
n = Node(s.key, s.value) # s要复制一份,不然待会儿s指向的节点,就被删掉了。n作为新的根
n.right = self._remove_min(node.right) # 删掉原s节点,并处理新根的右子树
n.left = node.left # 处理新根的左子树
del node
return n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
tree = BST()
tree.insert(6, '666')
tree.insert(2, '222')
tree.insert(3, '333')
tree.insert(4, '444')
tree.insert(1, '111')
print(tree.search(5))
print(tree.search(2))
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
None
222
tree.mid_order_visit()
1
1
2
3
4
6
tree.remove_min()
tree.mid_order_visit()
1
2
2
2
3
4
6
tree.remove_max()
tree.mid_order_visit()
1
2
2
2
3
4
tree.remove(2)
tree.mid_order_visit()
1
2
2
3
4
# 二叉搜索树的应用
找最大,找最小,找排序的前驱、后继,找floor、ceil。
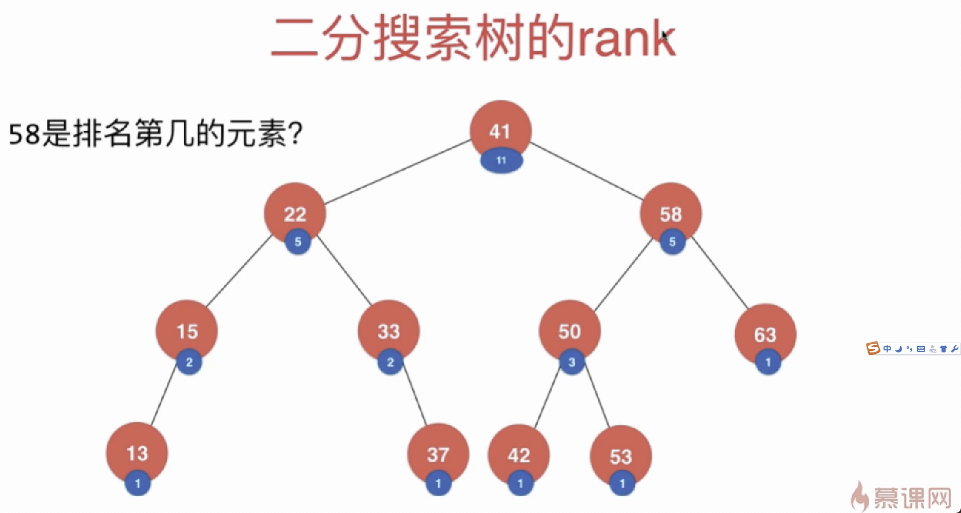
找rank。例如,key=58是从小到大排名第几的元素?不过这个需要额外在二分搜索树中每个节点增加一个信息,存放以该节点为根的子树中总的节点数目。这样以58为例,11-5+3=9,说明58前面一共有9个节点,58排名第10.
# 支持重复元素的二叉搜索树
1)修改树定义,定义左孩子为小于等于,右孩子为大于 2)修改节点定义,一个节点可存放多个重复的值
# 树的变种
二叉搜索树的局限性
由于插入顺序的不同,同样的数据,可能对应着不同的二叉搜索树的结构。例如,极端情况下,1,2,3,4,5,6,依次插入,则会形成一棵严重偏斜的树,所有节点都放在右子树,二叉搜索树退化为链表了。
解决方案 —— 平衡二叉树:(知名实现:红黑树,还有 2-3树,AVL树,splay树 等实现)。(左右两子树的高度差不超过1)
还有其他树:Treap(二叉搜索树和堆结合),trie(字典树,每个节点是一个字母,一条路径代表一个单词)
# 树形问题
# 递归方法,天然就有一种树的性质
例如归并排序和快速排序,不断从大到小分拆排序,就类似于树的形状。
搜索问题:例如决策树,通过树状遍历所有决策。
上次更新: 2022/11/11, 2:11:00