import math
import random

堆和堆排序

优先队列

普通队列是先进先出，时间先后；优先队列则与入队时间先后无关，而是根据优先级来出队。

优先队列的应用：例如，动态处理任务，每次选择最高优先级的任务来处理，与此同时会不断有新的任务加入，需要保证处理完当前任务后，下一个任务仍然是选择优先级最高的。又例如，有N个元素，选出排名前M个元素，如果先排序再选则O(nlogn)，而使用优先队列则可以达到O(nlogm)。

利用堆 可以实现优先队列。

堆

二叉堆：一棵二叉树，每个节点的值总是不大于其父节点的值（最大堆），且是一棵完全二叉树。

由于堆是完全二叉树，可以采用数组的方式来存储。从1开始标记根节点，则左子节点的下标，是父节点x2，右子节点的下标，是父节点x2+1。如果有某个元素下标为i，则其父节点的下标为 i//2。

向堆中加入元素

Shift-up的方法，即新的元素放在最后，然后该元素与其父节点比较大小，如果元素大于父节点，则互换，该元素再与其上级父节点比较大小，互换，直到元素小于父节点，或元素处于根节点位置。

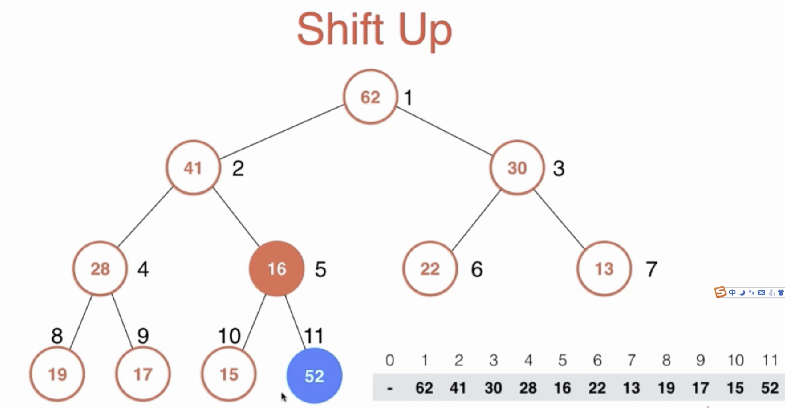
从堆中取出根节点元素 堆中只能取出根节点元素。取出根节点元素后，把原来最后一个元素放到根节点位置上，然后将根节点元素一点一点向下挪动调整。调整时，与左右两个孩子比较，如果没有左孩子，或者根比孩子都大，则结束调整；如果左孩子大，则根与左孩子交换，如果右孩子大，则根与右孩子交换。

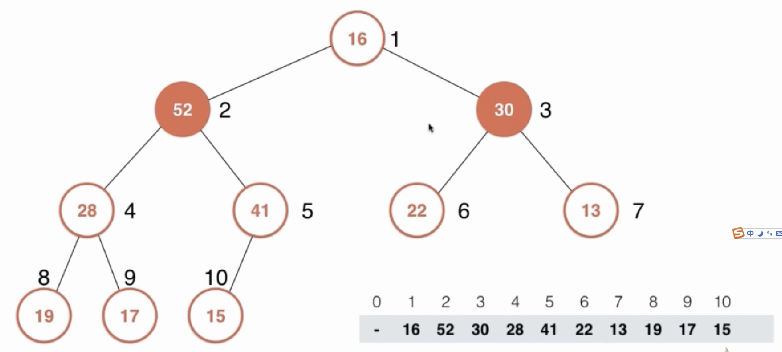
上移和下移操作，还可以进行一定的优化，类似之前插入排序时，寻找当前元素合适的插入位置，原本是每判断一个元素就进行一次位置交换（类似冒泡的感觉），后来优化改成先暂存当前元素，然后每判断一个元素就将元素后移，减少了swap的赋值次数。这里也可以采用这样的优化，以上移为例，记住当前元素的值，每次判断后，只将原来根的值覆盖当前元素位置，而不是进行交换，减少赋值次数。

import math
# 实现一个最大堆。
class MaxHeap(object):
    
    def __init__(self, arr=None):
        if arr:
            self._heapify(arr)
        else:
            self._data = [0, ] # 下标为0的位置不使用
    
    def _heapify(self, arr):
        self._data = [0, ]
        self._data.extend(arr)
        size = self.size()
        for i in range(size//2, 0, -1):
            self._shift_down(i)
    
    def size(self):
        return len(self._data) - 1
    
    def is_empty(self):
        return len(self._data) == 1
    
    def insert(self, item):
        self._data.append(item)
        self._shift_up(len(self._data) - 1)
        
    def _shift_up(self, index):
        while index > 1 and self._data[index//2] < self._data[index]:  # 与父元素比较大小并交换
            self._data[index//2], self._data[index] = self._data[index], self._data[index//2] 
            index = index // 2
            
    def pop(self):
        size = self.size()
        if size <= 0:
            return None
        result = self._data[1]
        self._data[1] = self._data[size]
        self._data.pop(-1)
        self._shift_down(1)
        return result
    
    def _shift_down(self, index):
        size = self.size()
        while 2 * index <= size:  # 节点有左孩子
            j = 2 * index  # 左孩子下标，也是当前标记两个孩子中较大值
            if j + 1 <= size and self._data[j+1] > self._data[j]:  # 有右孩子，且右孩子比左孩子大
                j += 1  # 将j变为右孩子下标，j仍然是当前标记两个孩子中的较大值
            if self._data[index] >= self._data[j]:  # 如果根比两个孩子都大，则结束
                break
            # 根与左右两孩子的较大值进行交换，且指针切到下一层
            self._data[index], self._data[j] = self._data[j], self._data[index]
            index = j

mh = MaxHeap()

for i in range(100):
    mh.insert(random.randint(0, 1000))
print(mh._data)

[0, 988, 977, 961, 973, 939, 904, 951, 969, 937, 884, 933, 847, 873, 566, 825, 770, 760, 877, 913, 651, 851, 840, 691, 756, 614, 631, 734, 450, 203, 625, 790, 410, 752, 211, 722, 403, 595, 300, 469, 350, 403, 789, 838, 759, 786, 449, 680, 499, 603, 566, 586, 73, 300, 433, 246, 367, 258, 51, 151, 101, 118, 1, 77, 68, 88, 426, 591, 68, 57, 93, 368, 140, 157, 99, 457, 59, 53, 180, 183, 19, 71, 211, 386, 341, 636, 570, 469, 500, 508, 84, 740, 432, 161, 145, 330, 10, 47, 359, 140, 119]

res = []
while not mh.is_empty():
    res.append(mh.pop())
print(res)

[988, 977, 973, 969, 961, 951, 939, 937, 933, 913, 904, 884, 877, 873, 851, 847, 840, 838, 825, 790, 789, 786, 770, 760, 759, 756, 752, 740, 734, 722, 691, 680, 651, 636, 631, 625, 614, 603, 595, 591, 586, 570, 566, 566, 508, 500, 499, 469, 469, 457, 450, 449, 433, 432, 426, 410, 403, 403, 386, 368, 367, 359, 350, 341, 330, 300, 300, 258, 246, 211, 211, 203, 183, 180, 161, 157, 151, 145, 140, 140, 119, 118, 101, 99, 93, 88, 84, 77, 73, 71, 68, 68, 59, 57, 53, 51, 47, 19, 10, 1]

如上所示，就可以利用堆来进行排序，先将无序的元素入堆，然后逐个取出堆顶元素，就是有序的了。

Heapify

是指将一个数组，经过变换 变成一个符合堆的要求的数组。 思路是，我们首先按照顺序，从这个数组中还原出堆。以下图为例，size为10，则 size//2 位置就是二叉树中第一个非叶子节点。叶子节点可以各自看做一个已经有序了的堆，所以只需要对每个非叶子节点进行整理，从下往上，使以每个非叶子节点为根的二叉树变为堆。整理的过程，其实就是 shift down的过程。

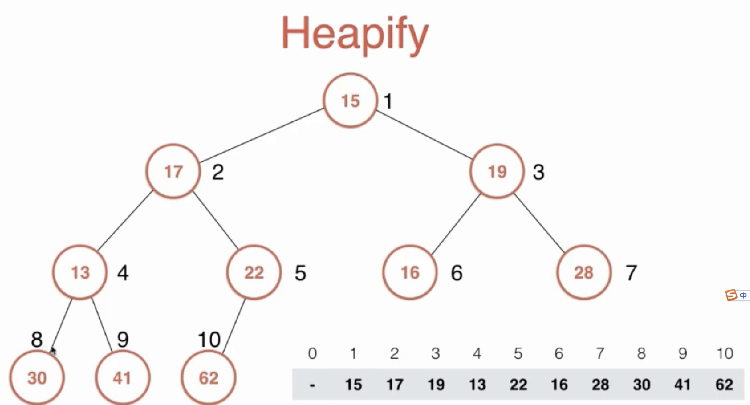
# heapify 示例
arr = [3, 9, 7, 2, 4, 6, 2, 8, 0]
hpi = MaxHeap(arr)
print(hpi._data)

[0, 9, 8, 7, 3, 4, 6, 2, 2, 0]

如果将元素逐个加入堆中，复杂度为O(nlogn)，因为共有n个元素，每个元素都要经过 logn 层的 shift up。而直接从数组heapify，时间复杂度居然只要O(n)。详细说明可以看这里：https://blog.csdn.net/mtawaken/article/details/7964914 思路大概是，只有一半的节点为非叶子节点，需要进行shift down，而每个节点shift down的次数是固定的（跟它所在的层有关，例如最底下的第一个非叶子节点，最多只需shift down一次）按照这样的公式加上点求极限之类就能算出总的时间复杂度了。

原地堆排序

前面的堆排序，给定一个数组，需要额外开辟一个同样大小的空间来存放堆。

可以通过原地堆排序的方式，直接给原数组排序。思路很简单，先将整个数组heapify，此时第一个就是最大的元素。将最大的元素和数组最后面的元素交换，则此时数组最后的元素是最大的元素。对除了最后一个元素之外，前面的部分继续heapify，继续取最大的元素与倒数第二个元素交换，继续把余下的前面部分heapify，直到只剩一个元素。此时，整个数组就从小到大排好序了。

具体实现上，还是之前heapify的方法，但这次是从下标0开始了，所以需要注意处理下标的关系。

原地堆排序由于不开辟额外空间，速度要比上面的堆排序略微快一丢丢。

def heap_sort(arr):
    n = len(arr)
    # 需要先 heapify 一次，使得0位置是最大的元素
    for i in range((n-1)//2, -1, -1): # 对非叶子节点进行shift down
        _shift_down(arr, n, i)
    # 逐个将最大元素从后往前排放，堆越来越小
    for i in range(n-1, 0, -1):
        # 将当前最头的元素放到后面排好序的部分的最前端，同时将此位置原来的元素放到堆顶
        arr[0], arr[i] = arr[i], arr[0]
        # 对余下的堆继续heapify。由于上一句操作其实只改变了当前堆顶的元素，所以只需将堆顶元素shift down一下，就相当于对整个堆heapify了。
        _shift_down(arr, i, 0)
    return arr

def _shift_down(arr, n, k):  # 思想上，与之前的shift down相同
    while 2 * k + 1 < n:
        j = 2 * k + 1
        if j + 1 < n and arr[j+1] > arr[j]:
            j += 1
        if arr[k] >= arr[j]:
            break
        arr[k], arr[j] = arr[j], arr[k]
        k = j

from random import randint
import time

def generate_data(max_num):
    return [randint(-max_num, max_num) for x in range(max_num)]

arr = generate_data(50000)

def check_sorted(arr):
    return all(arr[i] <= arr[i+1] for i in range(len(arr)-1))

def time_it(function, arr):
    start = time.clock()
    function(arr)
    end = time.clock()
    if not check_sorted(arr):
        print('sort result is not correct! ')
    print('time span = %f' % (end - start))

arr1 = arr[:]
time_it(heap_sort, arr1)

time span = 0.295670

排序算法总结

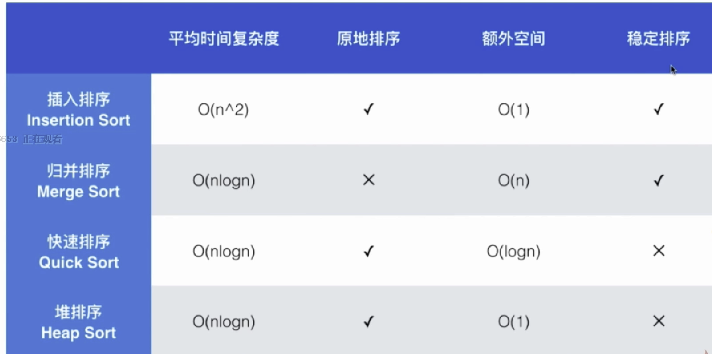
注意：快排的O(logn)空间，是指快排在递归过程中开辟的栈所要占用的空间。归并排序也要递归，所以其时间复杂度为O(n + logn)但在大O记法下，记作O(n)即可。

索引堆

之前的堆有一些问题

1）当元素是很长的字符串时，交换元素会造成大量消耗

2）当数组的下标和元素之间有对应关系时（例如操作系统进程调度，下标是进程id，元素值是优先级），进行构建堆的过程发生了元素值的交换，破坏了下标和元素之间原有的对应，想要将某个进程id的优先级提高，此时就已经找不到这种对应了。这个问题可以通过给元素值中再加一个字段（进程id）来解决，但这时如果想找到特定id的进程，不能直接通过下标找到，还要遍历一遍才行。

引入一种新的结构——索引堆，可以解决这两个问题。堆的整体思路不变，但额外区分开了index和data。在进行堆的构建时，比较大小使用的是data的值，而在进行移动时，将index中的值进行移动。这样既实现了元素交换，完成了堆的构建，又保持了下标和data的对应关系。

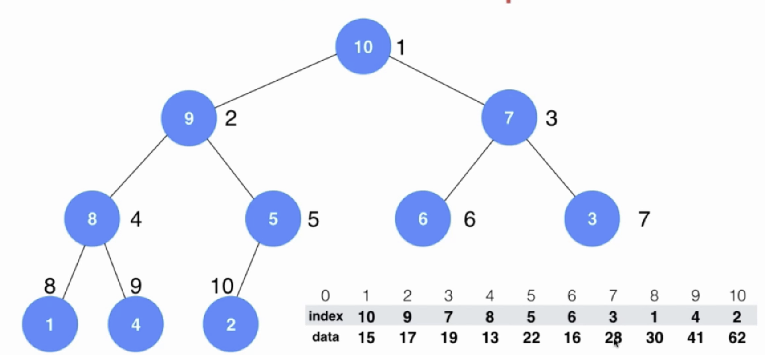
堆的一些应用

使用堆实现优先队列 系统进程的调度

在N个元素中选出最大的前M名 使用一个大小为M个的最小堆，逐个读取元素，先用M个元素建堆，之后每读到一个元素，判断是否入堆，入堆的话则将原来最小的元素出堆；读完全部元素N个之后，得到的堆就是最大的前M名。

多路归并排序 当归并有很多路时，可借助堆来快速找到各路当中最小的元素。