Dongxing's Wiki
  • 算法与数据结构
  • 算法与数据结构
anthony
2018-11-10
目录

算法与数据结构 | 高级排序

# 高级排序算法

时间复杂度更低的排序算法。

from random import randint
import time
1
2

辅助函数：生成测试数据

def generate_data(max_num):
    return [randint(-max_num, max_num) for x in range(max_num)]
1
2
arr = generate_data(50000)
1

辅助函数：测试排序是否正确

def check_sorted(arr):
    return all(arr[i] <= arr[i+1] for i in range(len(arr)-1))
1
2

辅助函数：测试用时

def time_it(function, arr):
    start = time.clock()
    function(arr)
    end = time.clock()
    if not check_sorted(arr):
        print('sort result is not correct! ')
    print('time span = %f' % (end - start))
1
2
3
4
5
6
7

# 归并排序

先逐层对半切分，直到最底层每一组只剩一个元素，然后从下往上进行归并，得到有序。归并时可借助额外的一份空间。

时间复杂度 nlog(n) ——共有 log(n)个层级，每个层级的复杂度为n。

def _merge(arr, l, mid, r):  # 将l-mid-r两段进行归并
    aux = arr[l: r+1]
    i = l
    j = mid + 1
    for k in range(l, r+1):
        if i > mid:
            arr[k] = aux[j-l]
            j += 1
        elif j > r:
            arr[k] = aux[i-l]
            i += 1
        elif aux[i-l] < aux[j-l]:
            arr[k] = aux[i-l]
            i += 1
        else:
            arr[k] = aux[j-l]
            j += 1
        

def _merge_sort(arr, l, r):  # merge sort递归。注意l，r表示当前组的左右边界，是闭区间。
    if l >= r:
        return None
    mid = (l+r) // 2
    _merge_sort(arr, l, mid)
    _merge_sort(arr, mid+1, r)
    _merge(arr, l, mid, r)
    

def merge_sort(arr):  # 入口
    _merge_sort(arr, 0, len(arr)-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
arr1 = arr[:]
time_it(merge_sort, arr1)
1
2
time span = 0.231756

# 归并排序的优化

对归并排序可以进行一定的优化：

1）如果左右两段，左边最右的元素已经小于右边最左的元素，说明两段其实已经有序了，无需再进行归并，可直接合并。

2）当要排序的数组比较短的时候，插入排序的效率反而可能更高（因为归并必须要归并到底，但数组较短的时候插入排序无需移动大量元素），所以可以设定当递归到某一层时，如果数组长度小于某个值，则将这一段采用插入排序 而非继续递归归并。

def _merge2(arr, l, mid, r):  # 将l-mid-r两段进行归并
    aux = arr[l: r+1]
    i = l
    j = mid + 1
    for k in range(l, r+1):
        if i > mid:
            arr[k] = aux[j-l]
            j += 1
        elif j > r:
            arr[k] = aux[i-l]
            i += 1
        elif aux[i-l] < aux[j-l]:
            arr[k] = aux[i-l]
            i += 1
        else:
            arr[k] = aux[j-l]
            j += 1

def _insertion_sort(arr, l, r):
    for i in range(l+1, r+1):
        position = i
        current = arr[i]
        while (arr[position-1] > current) and (position > l):
            arr[position] = arr[position-1]
            position -= 1
        arr[position] = current
    return arr 

def _merge_sort2(arr, l, r):  # merge sort递归。注意l，r表示当前组的左右边界，是闭区间。
    # 优化2：当数组长度小于15时，直接用插入排序来排这一段。
    if r - l <= 15:
        _insertion_sort(arr, l, r)
        return None
    
    mid = (l+r) // 2
    _merge_sort2(arr, l, mid)
    _merge_sort2(arr, mid+1, r)
    if arr[mid] > arr[mid+1]:  # 优化1：判断如果左边最大 小于等于 右边最小，则无需归并，否则进行归并。
        _merge2(arr, l, mid, r)
    

def merge_sort2(arr):  # 入口
    _merge_sort2(arr, 0, len(arr)-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
arr2 = arr[:]
time_it(merge_sort2, arr2)
1
2
time span = 0.187638

# 自底向上的归并排序

之前的方法是先从顶层递归划分，然后从下往上归并。 也可以直接从底层开始，两个元素为一组，依次归并往上。

def merge_sort_bu(arr):
    n = len(arr)
    size = 1
    while(size <= n):  # size尺寸逐个翻倍
        i = 0
        while(i < n):  # 对每一段进行归并
            _merge(arr, i, i+size-1, min(i+size+size-1, n-1))  # 直接调用之前的merge方法来归并
            i += size + size
        size += size
1
2
3
4
5
6
7
8
9
arr3 = arr[:]
time_it(merge_sort_bu, arr3)
1
2
time span = 0.232841

# 快速排序

总体思路类似于归并排序的分而治之，从大到小逐渐划分，并对每一小块进行排序，但归并是对半划分，快排则是有规律划分。

先以当前数组的第0下标元素为基准，将元素放到它在排序后的数组中应当处于的位置（叫做完成了一个Partition），则该元素之前的都是比它小的，之后的都是比它大的。再分别对前后两部分，继续应用这种操作，直到细分到最底，则整个数组完成排序。

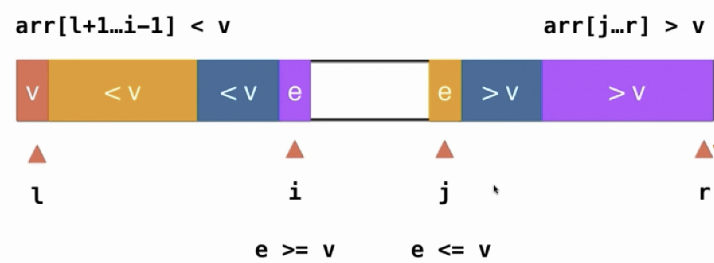
例如下图为一个 Partition 中的操作。考察下标l=0位置的元素v，另外使用下标j标记后面数组的分界点，i标记当前考察的元素。如果i的元素e大于v，则直接将其附在后面；如果i的元素e小于v，则交换i位置和j+1位置的元素，并将j往后挪动一格。这样，对i考察完之后，仍然保持前一部分数组元素都小于v，后一部分都大于v。然后将l位置与j位置交换，则完成了一趟操作，将值为v的元素放到了合适的位置。

代码看起来并不复杂，但一定要理解整个过程，且注意下标及越界的问题。

def _partition(arr, l, r):
    # 返回值 p 为切分点，且操作后使得 arr 中 l至p-1都小于p位置的值，p+1至r都大于p位置的值
    v = arr[l]
    # 设置标记变量j和i，使得整个过程中，arr[l+1...j]<v, arr[j+1...i)>v 注意前面写法中的区间开闭哦
    j = l
    for i in range(l+1, r+1):
        if arr[i] < v:
            arr[j+1], arr[i] = arr[i], arr[j+1]
            j += 1
        else:
            pass
    arr[l], arr[j] = arr[j], arr[l]
    return j

def _quick_sort(arr, l, r):
    if l >= r:
        return None
    p = _partition(arr, l, r)  # 先找到一个切分点
    _quick_sort(arr, l, p-1)  # 再分别对前后两部分递归调用排序
    _quick_sort(arr, p+1, r)
    
def quick_sort(arr):
    _quick_sort(arr, 0, len(arr)-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
arr4 = arr[:]
time_it(quick_sort, arr4)
1
2
time span = 0.170957

# 快速排序的优化：近乎有序的数组

优化1，类似于归并，当切分到数组比较小的时候，没必要再一直逐渐递归切分到底了，可以直接使用插入排序等方法，对短数组进行排序。

优化2，也是上面写法的快速排序的一个问题。当数组近乎有序的时候，如果用归并排序，总是一分为二，可以保证整个递归树的深度有限，但如果是快速排序，每次的切分，两半的大小并不相等，如果数组近乎有序，很有可能最左边的元素就是最小的元素，也就意味着在一次切分中，l..p-1是空的，p+1...r则包含了整个余下的部分。这样说来，面对近乎有序的数组，快速排序退化为了 O(n^2) 的算法，效率很低而且递归很深。

解决办法是，不再总是以最左侧的元素作为切分的标的，而是随机选择一个，这样避免了上面提到的近似有序的情况。

def _partition2(arr, l, r):
    # 优化2：不再以最左侧值为切分标的，而是随机选一个
    # 但是将该随机值与最左侧值进行交换，这样不用修改后面的代码逻辑。
    target = randint(l, r)
    arr[l], arr[target] = arr[target], arr[l]
    v = arr[l]
    j = l
    for i in range(l+1, r+1):
        if arr[i] < v:
            arr[j+1], arr[i] = arr[i], arr[j+1]
            j += 1
        else:
            pass
    arr[l], arr[j] = arr[j], arr[l]
    return j

def _insertion_sort2(arr, l, r):
    for i in range(l+1, r+1):
        position = i
        current = arr[i]
        while (arr[position-1] > current) and (position > l):
            arr[position] = arr[position-1]
            position -= 1
        arr[position] = current
    return arr 

def _quick_sort2(arr, l, r):
    if r - l < 15:
        _insertion_sort2(arr, l, r)  # 优化1：短数组直接用插入排序来排。
        return None
    p = _partition2(arr, l, r)
    _quick_sort2(arr, l, p-1)  
    _quick_sort2(arr, p+1, r)
    
def quick_sort2(arr):
    _quick_sort2(arr, 0, len(arr)-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
arr5 = arr[:]
time_it(quick_sort2, arr5)
1
2
time span = 0.158590

# 快速排序的再次改进：大量重复值

上面改进了对于近似有序的数组，快速排序应该如何改进。但另外还有一种情况，如果数组中存在大量重复值，每次切分仍然会可能导致两半大小极度不平衡，退化到O(n^2)。

采用下面的方法来改进算法，以避免此问题。仍然是随机选择一个v并将其值交换存到数组下标0的位置中。但这次不再从左往右，而是从两端往中间操作。两个指针i，j往中间读取，直到i位置的元素>=v，而j位置的元素<=v，则ij进行交换，继续读取，直到ij重合。

这种读法的好处在于，对于=v的元素，仍然会被交换位置，而不是使得=v的元素集中在某一侧，避免了大量重复值时的切分不平衡。

def _partition3(arr, l, r):
    target = randint(l, r)
    arr[l], arr[target] = arr[target], arr[l]
    v = arr[l]
    
    # arr[l+1, i) <= v, arr(j...r] >= v
    i = l + 1
    j = r
    while True:
        while i <= r and arr[i] < v:
            i += 1
        while j >= l+1 and arr[j] > v:
            j -= 1
        if i > j:
            break
        arr[i], arr[j] = arr[j], arr[i]
        i += 1
        j -= 1
    arr[l], arr[j] = arr[j], arr[l]
    return j

def _insertion_sort3(arr, l, r):
    for i in range(l+1, r+1):
        position = i
        current = arr[i]
        while (arr[position-1] > current) and (position > l):
            arr[position] = arr[position-1]
            position -= 1
        arr[position] = current
    return arr 

def _quick_sort3(arr, l, r):
    if r - l < 15:
        _insertion_sort3(arr, l, r)
        return None
    p = _partition3(arr, l, r)
    _quick_sort3(arr, l, p-1)  
    _quick_sort3(arr, p+1, r)
    
def quick_sort3(arr):
    _quick_sort3(arr, 0, len(arr)-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
arr6 = arr[:]
time_it(quick_sort3, arr6)
1
2
time span = 0.149566

# 快速排序的继续改进：三路快速排序

将数组分成三部分：<v, =v, >v三部分。而优势在于，对于 =v 的部分，不再需要参与后续的排序了。

如下图所示的排序。当前e等于v，则直接i++即可；如果e小于v，则lt+1位置和i位置交换，i++，lt++；如果e大于v，gt-1位置和i位置交换，gt--，i不要改变。直到i和gt重合。然后将l位置和lt位置交换，则完成了一趟排序。接下来只需要对<v和>v的两个部分进行排序。

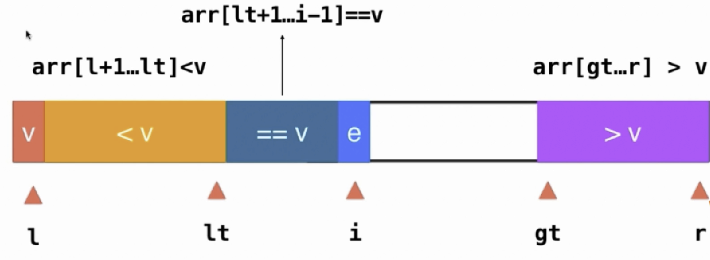
这一方法可能是目前很多库中默认使用的快排方案。虽然对于一般的数组，其速度未必比其他方法快，但在处理有大量重复值的数组时其性能表现显著。

def _partition4(arr, l, r):
    target = randint(l, r)
    arr[l], arr[target] = arr[target], arr[l]
    v = arr[l]
    
    # arr[l+1...lt] < v
    lt = l
    # arr[gt...r] > v
    gt = r + 1
    # arr[lt+1...i) == v
    i = l + 1
    while i < gt:
        if arr[i] < v:
            arr[i], arr[lt+1] = arr[lt+1], arr[i]
            lt += 1
            i += 1
        elif arr[i] > v:
            arr[i], arr[gt-1] = arr[gt-1], arr[i]
            gt -= 1
        else:
            i += 1
    arr[l], arr[lt] = arr[lt], arr[l]
    return lt, gt

def _insertion_sort4(arr, l, r):
    for i in range(l+1, r+1):
        position = i
        current = arr[i]
        while (arr[position-1] > current) and (position > l):
            arr[position] = arr[position-1]
            position -= 1
        arr[position] = current
    return arr 

def _quick_sort4(arr, l, r):
    if r - l < 15:
        _insertion_sort4(arr, l, r)
        return None
    lt, gt = _partition4(arr, l, r)
    _quick_sort4(arr, l, lt-1)  
    _quick_sort4(arr, gt, r)
    
def quick_sort4(arr):
    _quick_sort4(arr, 0, len(arr)-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
arr7 = arr[:]
time_it(quick_sort4, arr7)
1
2
time span = 0.236500
1

# 归并排序和快速排序的衍生问题

# 分治算法的思想

将原问题分割成同等结构的子问题，将子问题解决后，原问题也就得到了解决。 归并排序的分割方法是简单的对半分，但在归并时要多考虑一些；快排在分割方面下了很大功夫，合并就不需要做什么了。

# 利用归并和快排思路，解决算法问题

逆序对 问题 求数组中的逆序对的个数。思路是利用归并排序，在每一次两路归并时，有左右两半，如果左边的元素大于右边的当前元素，则说明存在逆序，逆序对的个数为左边剩下的元素的个数。 详细可见：剑指Offer题解 (opens new window)

数组中第k大的元素 如果是取最大或最小，思路是直接遍历一遍找到最大最小，复杂度O(n)。但如果是第k大，一种思路是整个数组排序，复杂度是O(nlogn)，即排序的复杂度，另一种思路是利用快排的思路，以O(n)的复杂度完成。

快排中，每一个Partition时，会随机选一个元素，并为该元素找到它最终的位置，然后将前后两半继续快排。那么我们可以先随机选一个元素，找到它的位置，例如k为100，元素的位置为90，那么后面继续快排的时候，就只需要将该90下标元素的后半部分进行快排，假如下次找到的元素位置为110，则只需要将91-109的部分进行快排，直到找到下标100位置的元素。整个复杂度=n + n/2 + n/4 + n/8 ... + 1 ~= O(2n)。

上次更新: 2022/11/11, 2:11:00
基础排序
算法与数据结构 | 堆和堆排序

← 算法与数据结构 | 堆和堆排序→

Theme by Vdoing | Copyright © 2017-2023 anthony 京ICP备17072417-3